题目内容
11.已知定义在R上的函数f(x)=|x-a2|+|x+4|的最小值为4a.(1)求a的值;
(2)不等式|x-a|-|x+a|≤|b+1|对任意的x∈R恒成立,求实数b的取值范围.
分析 (1)由条件利用绝对值的意义求得f(x)=|x-a2|+|x+4|的最小值,再根据它的最小值为4a,从而求得a的值.
(2)求得|x-a|-|x+a|的最大值为4,可得4≤|b+1|,由此求得b的范围.
解答 解:(1)由题意可得函数f(x)=|x-a2|+|x+4|≥|a2+4|,故它的最小值为|a2+4|,
再根据它的最小值为4a,可得|a2+4|=4a,即a2+4=4a,求得a=2.
(2)不等式|x-2|-|x+2|表示数轴上的x对应点到2对应点的距离减去它到-2对应点的距离,它的最大值为4,
不等式|x-a|-|x+a|≤|b+1|对任意的x∈R恒成立,可得4≤|b+1|,即b+1≥4,或b+1≤-4,
求得b≥3,或 b≤-5.
点评 本题主要考查绝对值的意义,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
11.若$\root{n}{{a}^{n}}$+($\root{n+1}{a}$)n+1=0,a≠0,且n∈N*,则( )
| A. | a>0且n为偶数 | B. | a<0且n为偶数 | C. | a>0且n为奇数 | D. | a<0且n为奇数 |
16.已知三个函数f(x)=2x+x,g(x)=x-2,h(x)=log2x+x的零点依次为a,b,c,则( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.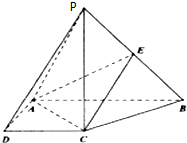 如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.