题目内容
(本小题满分13分)
已知数列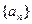 ,其前
,其前 项和为
项和为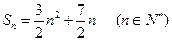 .
.
(1)求数列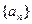 的通项公式,并证明数列
的通项公式,并证明数列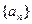 是等差数列;
是等差数列;
(2)如果数列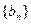 满足
满足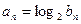 ,请证明数列
,请证明数列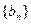 是等比数列;
是等比数列;
(3)设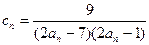 ,数列
,数列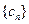 的前
的前 项和为
项和为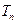 ,求使不等式
,求使不等式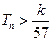 对一切
对一切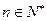 都成立的最大正整数
都成立的最大正整数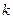 的值.
的值.
已知数列
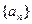 ,其前
,其前 项和为
项和为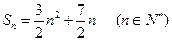 .
.(1)求数列
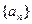 的通项公式,并证明数列
的通项公式,并证明数列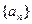 是等差数列;
是等差数列;(2)如果数列
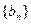 满足
满足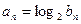 ,请证明数列
,请证明数列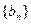 是等比数列;
是等比数列;(3)设
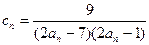 ,数列
,数列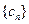 的前
的前 项和为
项和为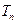 ,求使不等式
,求使不等式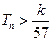 对一切
对一切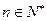 都成立的最大正整数
都成立的最大正整数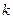 的值.
的值.解:(Ⅰ)当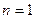 时,
时,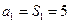 , ………………………1分
, ………………………1分
当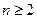 时,
时,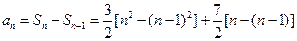
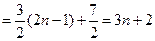 . ……………………………2分
. ……………………………2分
又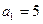 满足
满足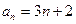 , ……………………………3分
, ……………………………3分
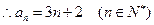 . ………………………………4分
. ………………………………4分
∵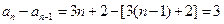
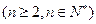 ,
,
∴数列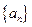 是以5为首项,
是以5为首项,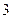 为公差的等差数列. …
为公差的等差数列. … ……………5分
……………5分
(Ⅱ)由已知得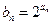
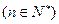 , ………………………6分
, ………………………6分
∵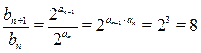
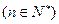 , ……………………7分
, ……………………7分
又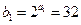 ,
,
∴数列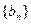 是以
是以 为首项,
为首项,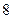 为公比的等比数列. ………………8分
为公比的等比数列. ………………8分
(Ⅲ)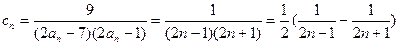 ……10分
……10分
∴
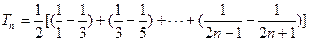
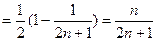 . ……………………11分
. ……………………11分
∵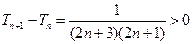
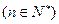 ,
,
∴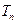 单调递增.
单调递增.
∴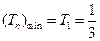 . …………………12分
. …………………12分
∴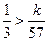 ,解得
,解得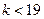 ,因为
,因为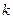 是正整数, ∴
是正整数, ∴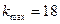 . ………………13分
. ………………13分
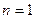 时,
时,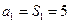 , ………………………1分
, ………………………1分当
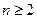 时,
时,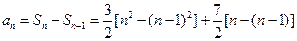
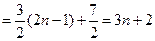 . ……………………………2分
. ……………………………2分又
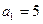 满足
满足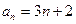 , ……………………………3分
, ……………………………3分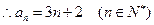 . ………………………………4分
. ………………………………4分∵
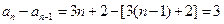
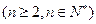 ,
,∴数列
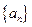 是以5为首项,
是以5为首项,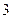 为公差的等差数列. …
为公差的等差数列. … ……………5分
……………5分(Ⅱ)由已知得
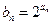
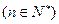 , ………………………6分
, ………………………6分∵
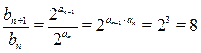
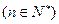 , ……………………7分
, ……………………7分又
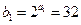 ,
, ∴数列
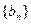 是以
是以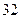 为首项,
为首项,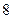 为公比的等比数列. ………………8分
为公比的等比数列. ………………8分(Ⅲ)
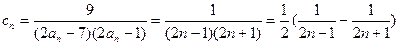 ……10分
……10分∴

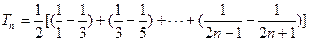
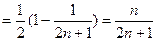 . ……………………11分
. ……………………11分∵
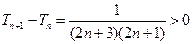
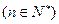 ,
, ∴
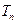 单调递增.
单调递增. ∴
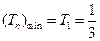 . …………………12分
. …………………12分∴
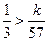 ,解得
,解得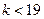 ,因为
,因为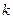 是正整数, ∴
是正整数, ∴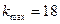 . ………………13分
. ………………13分略

练习册系列答案
相关题目
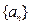 是一等差数列,数列
是一等差数列,数列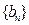 的前n项和为
的前n项和为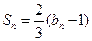 ,若
,若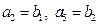 .
.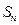 .
.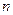 项和为
项和为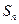 ,且
,且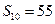 ,
,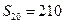 .
.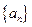 的通项公式;
的通项公式;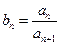 ,是否存在
,是否存在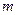 、
、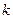
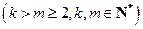 ,使得
,使得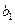 、
、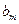 、
、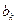 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的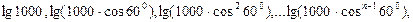 …的前_____项和为最大?
…的前_____项和为最大?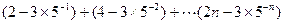 =_
=_ _________ .
_________ .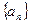 的首项
的首项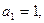 前
前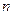 项和为
项和为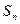 ,且满足
,且满足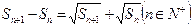 .
.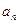
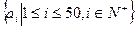 取出三个数构成以正整数为公比的递增等比数列,放回后再取出三个数构成以正整数为公比的递增等比数列,相同的数列只取一次,按照上述取法取下去,直到取完所有满足条件的数列为止。求满足上述条件的所有的不同数列的和M.
取出三个数构成以正整数为公比的递增等比数列,放回后再取出三个数构成以正整数为公比的递增等比数列,相同的数列只取一次,按照上述取法取下去,直到取完所有满足条件的数列为止。求满足上述条件的所有的不同数列的和M. 设
设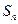 是等差数列
是等差数列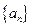 的前
的前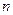 项和,若
项和,若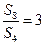 ,则
,则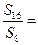 ( )
( )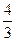

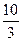
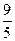
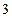
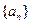 和
和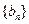 满足:
满足: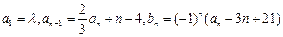 ,其中
,其中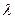 为实数,n为正整数,数列
为实数,n为正整数,数列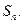
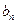 ,并求
,并求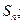
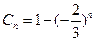 ,试求数列
,试求数列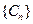 的最大项和最小项;
的最大项和最小项;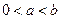 ,是否存在实数
,是否存在实数 使得对任意实数n,都有
使得对任意实数n,都有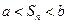 成立?若存在,求
成立?若存在,求