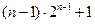题目内容
(本小题满分14分)
已知等差数列{an}的前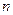 项和为
项和为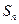 ,且
,且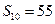 ,
,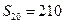 .
.
(1)求数列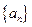 的通项公式;
的通项公式;
(2)设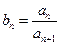 ,是否存在
,是否存在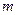 、
、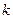
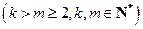 ,使得
,使得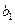 、
、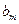 、
、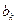 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的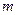 、
、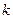 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知等差数列{an}的前
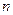 项和为
项和为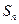 ,且
,且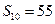 ,
,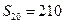 .
.(1)求数列
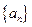 的通项公式;
的通项公式;(2)设
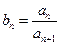 ,是否存在
,是否存在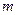 、
、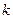
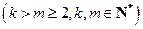 ,使得
,使得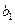 、
、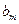 、
、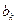 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的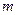 、
、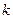 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(本小题主要考查等差数列、等比数列、不等式等基础知识,考查方程思想以及运算求解能力.)
解:(1)设等差数列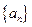 的公差为
的公差为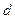 ,则
,则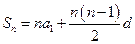 .………………………………………1分
.………………………………………1分
由已知,得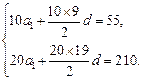 ………………………………………………………………………3分
………………………………………………………………………3分
即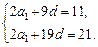 解得
解得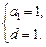 …………………………………………………………………………5分
…………………………………………………………………………5分
所以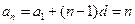 (
(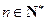 ).………………………………………………………………6分
).………………………………………………………………6分
(2)假设存在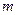 、
、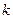
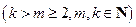 ,使得
,使得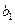 、
、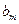 、
、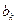 成等比数列,
成等比数列,
则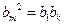 .……………………………………………………………………………………………7分
.……………………………………………………………………………………………7分
因为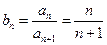 ,…………………………………………………………………………………8分
,…………………………………………………………………………………8分
所以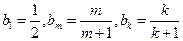 .
.
所以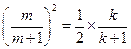 .……………………………………………………………………………9分
.……………………………………………………………………………9分
整理,得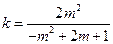 .…………………………………………………………………………10分
.…………………………………………………………………………10分
以下给出求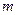 ,
,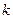 的三种方法:
的三种方法:
方法1:因为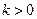 ,所以
,所以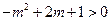 .………………………………………………………11分
.………………………………………………………11分
解得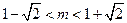 .……………………………………………………………………………12分
.……………………………………………………………………………12分
因为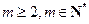 ,
,
所以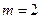 ,此时
,此时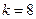 .
.
故存在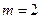 、
、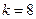 ,使得
,使得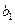 、
、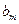 、
、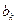 成等比数列.……………………………………………14分
成等比数列.……………………………………………14分
方法2:因为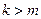 ,所以
,所以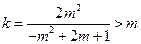 .…………………………………………………11分
.…………………………………………………11分
即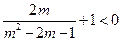 ,即
,即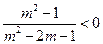 .
.
解得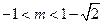 或
或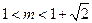 .………………………………………………………………12分
.………………………………………………………………12分
因为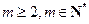 ,
,
所以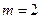 ,此时
,此时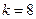 .
.
故存在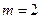 、
、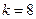 ,使得
,使得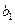 、
、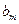 、
、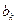 成等比数列.……………………………………………14分
成等比数列.……………………………………………14分
方法3:因为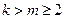 ,所以
,所以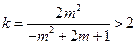 .……………………………………………11分
.……………………………………………11分
即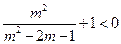 ,即
,即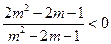 .
.
解得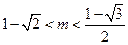 或
或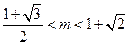 .…………………………………………………12分
.…………………………………………………12分
因为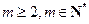 ,
,
所以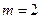 ,此时
,此时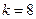 .
.
故存在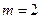 、
、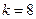 ,使得
,使得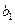 、
、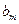 、
、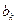 成等比数列.……………………………………………14分
成等比数列.……………………………………………14分
解:(1)设等差数列
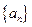 的公差为
的公差为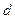 ,则
,则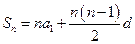 .………………………………………1分
.………………………………………1分由已知,得
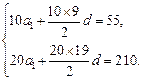 ………………………………………………………………………3分
………………………………………………………………………3分即
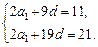 解得
解得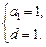 …………………………………………………………………………5分
…………………………………………………………………………5分所以
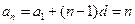 (
(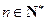 ).………………………………………………………………6分
).………………………………………………………………6分(2)假设存在
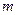 、
、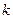
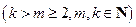 ,使得
,使得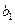 、
、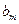 、
、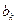 成等比数列,
成等比数列,则
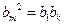 .……………………………………………………………………………………………7分
.……………………………………………………………………………………………7分因为
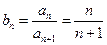 ,…………………………………………………………………………………8分
,…………………………………………………………………………………8分所以
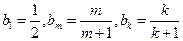 .
.所以
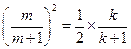 .……………………………………………………………………………9分
.……………………………………………………………………………9分整理,得
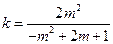 .…………………………………………………………………………10分
.…………………………………………………………………………10分以下给出求
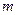 ,
,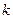 的三种方法:
的三种方法:方法1:因为
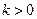 ,所以
,所以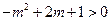 .………………………………………………………11分
.………………………………………………………11分解得
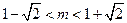 .……………………………………………………………………………12分
.……………………………………………………………………………12分因为
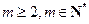 ,
,所以
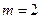 ,此时
,此时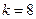 .
.故存在
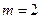 、
、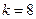 ,使得
,使得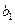 、
、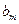 、
、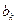 成等比数列.……………………………………………14分
成等比数列.……………………………………………14分方法2:因为
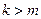 ,所以
,所以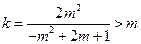 .…………………………………………………11分
.…………………………………………………11分即
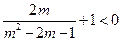 ,即
,即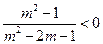 .
.解得
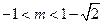 或
或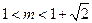 .………………………………………………………………12分
.………………………………………………………………12分因为
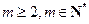 ,
,所以
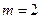 ,此时
,此时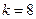 .
.故存在
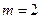 、
、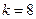 ,使得
,使得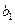 、
、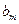 、
、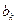 成等比数列.……………………………………………14分
成等比数列.……………………………………………14分方法3:因为
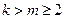 ,所以
,所以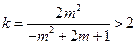 .……………………………………………11分
.……………………………………………11分即
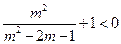 ,即
,即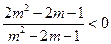 .
.解得
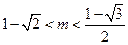 或
或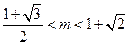 .…………………………………………………12分
.…………………………………………………12分因为
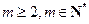 ,
,所以
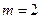 ,此时
,此时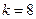 .
.故存在
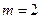 、
、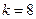 ,使得
,使得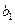 、
、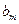 、
、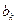 成等比数列.……………………………………………14分
成等比数列.……………………………………………14分略

练习册系列答案
相关题目
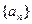 ,其前
,其前 项和为
项和为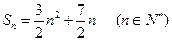 .
.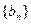 满足
满足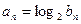 ,请证明数列
,请证明数列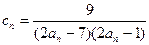 ,数列
,数列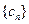 的前
的前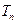 ,求使不等式
,求使不等式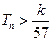 对一切
对一切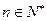 都成立的最大正整数
都成立的最大正整数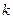 的值.
的值.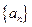 是公比为
是公比为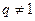 的等比数列,且
的等比数列,且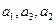 成等差数列.
成等差数列.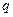 的值;
的值; 是以2为首项,
是以2为首项,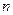 项和为
项和为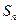 ,求使
,求使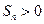 成立的
成立的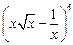 的二项展开式中的第5项的值等于5,数列
的二项展开式中的第5项的值等于5,数列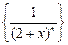 的前n项为
的前n项为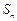 ,则
,则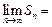 .
.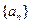 的前n项和
的前n项和 ,则
,则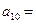 ▲
▲ 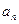 }中,
}中,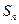 是它的前n项和,且
是它的前n项和,且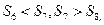 有下列四个命题:
有下列四个命题: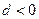 ;②
;②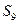 一定小于
一定小于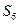 ;
;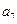 是各项中最
是各项中最 大的一项目;④
大的一项目;④ 一定是
一定是
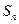 是等差数列{
是等差数列{ 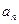 }的前n项和,若
}的前n项和,若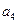 ="9,"
="9," 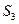 =15,则数列{
=15,则数列{ 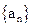 的通项公式为
的通项公式为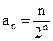 ,则前
,则前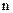 项和为( )
项和为( )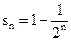 B
B 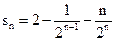 C
C 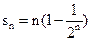 D
D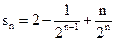
 满足:
满足: ,则
,则 ( )
( )