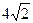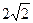题目内容
O为坐标原点, 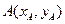 和
和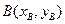 两点分别在射线
两点分别在射线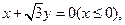
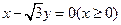 上移动,且
上移动,且 ,动点P满足
,动点P满足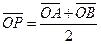 ,
,
记点P的轨迹为C.
(I)求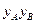 的值;
的值;
(II)求P点的轨迹C的方程,并说明它表示怎样的曲线?
(III)设点G(-1,0),若直线 与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求
与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求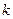 的取值范围.
的取值范围.
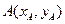 和
和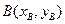 两点分别在射线
两点分别在射线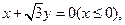
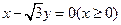 上移动,且
上移动,且 ,动点P满足
,动点P满足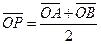 ,
,记点P的轨迹为C.
(I)求
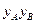 的值;
的值;(II)求P点的轨迹C的方程,并说明它表示怎样的曲线?
(III)设点G(-1,0),若直线
 与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求
与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求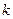 的取值范围.
的取值范围.(I)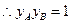
(II)轨迹C的方程为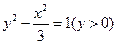 ,它表示焦点在
,它表示焦点在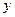 轴上的双曲线.
轴上的双曲线.
(III)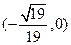
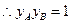
(II)轨迹C的方程为
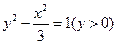 ,它表示焦点在
,它表示焦点在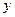 轴上的双曲线.
轴上的双曲线.(III)
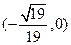
(I) ∵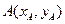 ,
,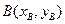 分别在射线
分别在射线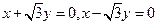 上,
上,
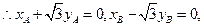
即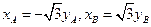 ,
,
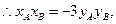
又∵
 .
.
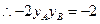 ,
, 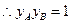 .
.
(II) 设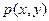 由
由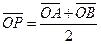 可得
可得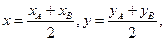
即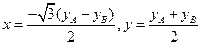
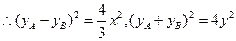
两式相减有: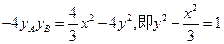 .
.
∵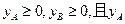 、
、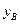 不同时为0,
不同时为0, 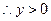
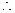 轨迹C的方程为
轨迹C的方程为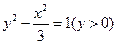 ,它表示焦点在
,它表示焦点在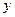 轴上的双曲线.
轴上的双曲线.
(III)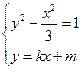
消去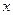 ,整理得:
,整理得: 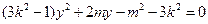 .
.
∵直线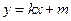 与曲线C交于M、N两点,
与曲线C交于M、N两点,
设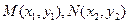
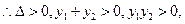
即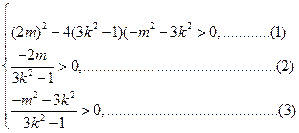
由(1)整理得: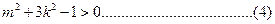
由(3)有: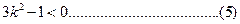
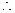 由(2)有
由(2)有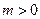 .
.
又∵M、N在以点G为圆心的圆上,
设MN的中点为Q,则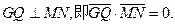
∵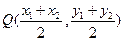 ,
,
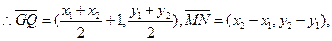
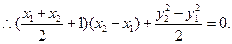
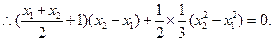
∵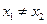
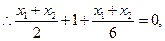
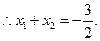
又∵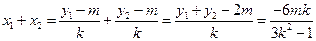
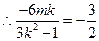 .
.
整理得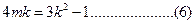
把(6)代入(4)中有: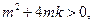
由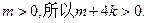
又由(6)有
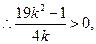
∵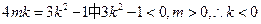
于是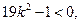
解得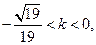
再由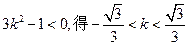 .
.
综合得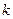 的取值范围为
的取值范围为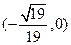
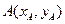 ,
,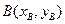 分别在射线
分别在射线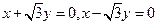 上,
上,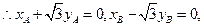
即
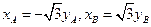 ,
,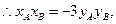
又∵

 .
.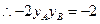 ,
, 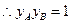 .
.(II) 设
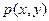 由
由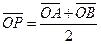 可得
可得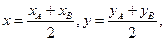
即
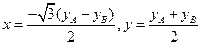
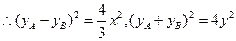
两式相减有:
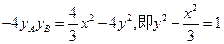 .
.∵
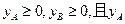 、
、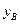 不同时为0,
不同时为0, 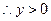
 轨迹C的方程为
轨迹C的方程为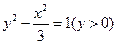 ,它表示焦点在
,它表示焦点在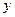 轴上的双曲线.
轴上的双曲线.(III)
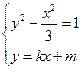
消去
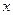 ,整理得:
,整理得: 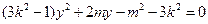 .
.∵直线
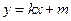 与曲线C交于M、N两点,
与曲线C交于M、N两点,设
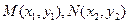
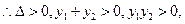
即
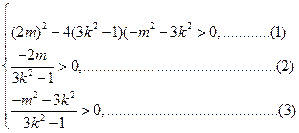
由(1)整理得:
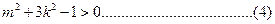
由(3)有:
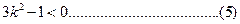
 由(2)有
由(2)有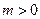 .
.又∵M、N在以点G为圆心的圆上,
设MN的中点为Q,则
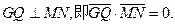
∵
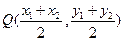 ,
,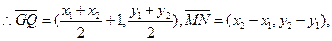
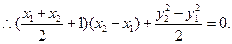
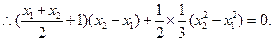
∵
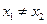
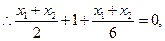
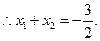
又∵
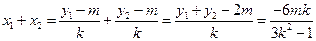
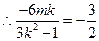 .
.整理得
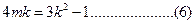
把(6)代入(4)中有:
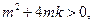
由
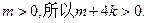
又由(6)有

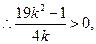
∵
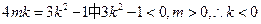
于是
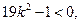
解得
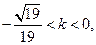
再由
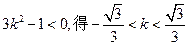 .
.综合得
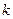 的取值范围为
的取值范围为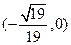

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
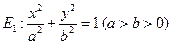 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点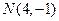 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为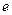 ,求
,求 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.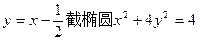
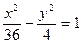
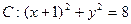 ,定点
,定点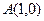 ,
,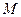 为圆上一动点,点
为圆上一动点,点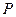 在
在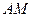 上,点
上,点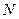 在
在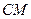 上,且满足
上,且满足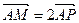 ,
,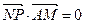 ,点
,点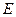 .
.
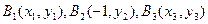 在曲线
在曲线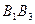 的垂直平分线为直线
的垂直平分线为直线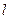 ,且
,且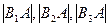 成等差数列,求
成等差数列,求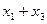 的值,并证明直线
的值,并证明直线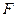 (0,2)的直线交曲线
(0,2)的直线交曲线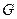 、
、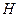 (点
(点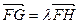 ,求
,求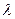 的取值范围.
的取值范围.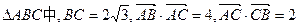 ,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
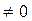 使|OF|=|OG|
使|OF|=|OG|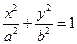
 的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点
的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点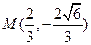 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.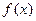 在定义域(-1,1)内可导,且
在定义域(-1,1)内可导,且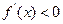 ,点A(1,
,点A(1,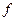 (
(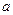 ));B(
));B(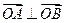 成立,试在
成立,试在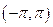 内求满足不等式
内求满足不等式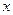 cos
cos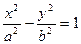 的离心率为
的离心率为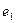 ,双曲线
,双曲线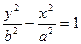 的离心率为
的离心率为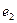 ,则
,则