题目内容
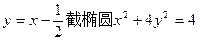
解法一 设直线与椭圆交于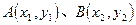 两点。
两点。
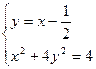
消去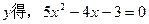 ①
①
方程①的判别式 ,
,
由韦达定理,
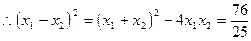
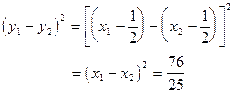
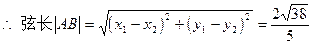
解法二:由解法一中得到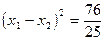

由弦长公式
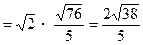
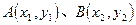 两点。
两点。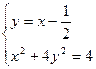
消去
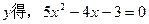 ①
①方程①的判别式
 ,
,由韦达定理,

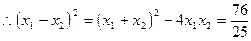
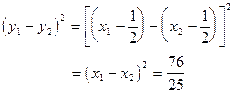
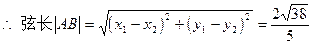
解法二:由解法一中得到
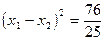

由弦长公式

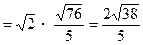
求直线与圆锥曲线相交所截得的弦长,可以联立它们的方程,解方程组求出交点坐标,再利用两点间的距离公式即可求出,但计算比较麻烦。如果在方程组消元后得到一元二次方程,利用韦达定理可简化计算,也可用弦长公式求解。
求直线与圆锥曲线相交截得弦长的有关问题,是一类重要的题型,弦长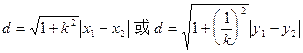 ,可做为公式用,但必须知道其公式推导的基础是两点间距离公式和一元二次方程的根与系数的关系。
,可做为公式用,但必须知道其公式推导的基础是两点间距离公式和一元二次方程的根与系数的关系。
求直线与圆锥曲线相交截得弦长的有关问题,是一类重要的题型,弦长
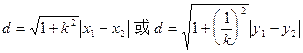 ,可做为公式用,但必须知道其公式推导的基础是两点间距离公式和一元二次方程的根与系数的关系。
,可做为公式用,但必须知道其公式推导的基础是两点间距离公式和一元二次方程的根与系数的关系。
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
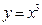 在
在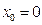 处的切线是否存在,若存在,求出切线的斜率和切线方程;若不存在,请说明理由.
处的切线是否存在,若存在,求出切线的斜率和切线方程;若不存在,请说明理由.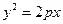 的焦点与双曲线
的焦点与双曲线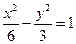 的右焦点重合,则
的右焦点重合,则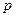 的值为 .
的值为 .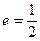
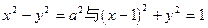
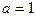
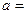 0
0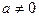
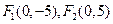 ,点
,点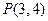 是双曲线的渐近线与椭圆的一个交点,求双曲线与椭圆的方程。
是双曲线的渐近线与椭圆的一个交点,求双曲线与椭圆的方程。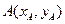 和
和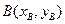 两点分别在射线
两点分别在射线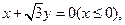
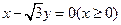 上移动,且
上移动,且 ,动点P满足
,动点P满足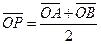 ,
,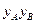 的值;
的值; 与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求
与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求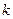 的取值范围.
的取值范围.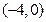 ,
,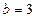 ,其焦点在
,其焦点在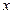 轴上,则该椭圆的标准方程为 。
轴上,则该椭圆的标准方程为 。