题目内容

12．已知函数f（x）=x2-|x|+3，f（|x|）=a有实根，求a的取值范围．

分析 化简f（|x|）=x2-|x|+3，从而化f（|x|）=a有实根为函数f（|x|）=x2-|x|+3的最值问题，从而作图求解．

解答 解：∵f（x）=x2-|x|+3，
∴f（|x|）=|x|2-|x|+3=x2-|x|+3，
作函数f（|x|）=x2-|x|+3的图象如下，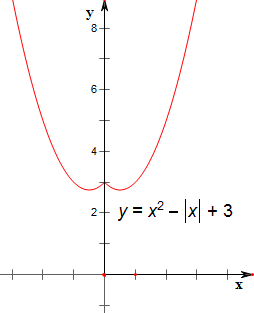

结合函数的图象可知，
当|x|=$\frac{1}{2}$时，f（|x|）有最小值2+$\frac{3}{4}$=$\frac{11}{4}$；
故若f（|x|）=a有实根，
则a≥$\frac{11}{4}$．

点评 本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用，属于中档题．

练习册系列答案
相关题目
2．在△ABC中，已知a=4，b=x，A=60°，如果解该三角形有两解，则（　　）
A．x＞4B．0＜x≤4C．x≤$\frac{8\sqrt{3}}{3}$D．4＜x＜$\frac{8\sqrt{3}}{3}$
3．已知f（x）=sin（$\frac{π}{4}$-2x），要使不等式|f（x）-m|＜1对任意x∈R都成立，求实数m的取值范围．
20．化简：$\frac{{x}^{2}+3x+9}{{x}^{3}-27}$+$\frac{6x}{9x-{x}^{2}}$-$\frac{x-1}{6+2x}$．
7．已知函数f（x）的定义域为D，区间I⊆D，若存在常数L，使得对任意x1，x2∈I，都有|f（x1）-f（x2）|≤L|x1-x2|，则称函数f（x）在区间I上满足李普希兹（Lipschitz）条件，已知f（x）=x2ex在区间（-∞，1]上满足李普希兹条件，则L的最小值是（　　）
A．3eB．2eC．eD．1
1．如图是一个方程为$\frac{x^2}{4}$+y2=1的椭圆，则由过上、下顶点和两焦点的四条直线围成图形的面积为2$\sqrt{3}$．
8．已知P为椭圆$\frac{x^2}{4}+{y^2}$=1上的任意一点，O为坐标原点，M在线段OP上，且$\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OP}$
（Ⅰ）求点M的轨迹方程；
（Ⅱ）已知直线3x+6y-2=0与M的轨迹相交于A，B两点，求△OAB的面积．
5．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，斜率为1的直线过F且交椭圆于A、B两点，若$\overrightarrow{OA}$+$\overrightarrow{OB}$与$\overrightarrow{a}$=（3，-1）共线，则此椭圆的离心率为$\frac{\sqrt{6}}{3}$．
6．曲线y=ex上的点到直线y=x的距离的最小值是（　　）
A．$\frac{{\sqrt{2}}}{2}$B．$\sqrt{2}$C．$\frac{e}{2}$D．$\frac{{\sqrt{e}}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网