题目内容
5.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,斜率为1的直线过F且交椭圆于A、B两点,若$\overrightarrow{OA}$+$\overrightarrow{OB}$与$\overrightarrow{a}$=(3,-1)共线,则此椭圆的离心率为$\frac{\sqrt{6}}{3}$.分析 直线与椭圆方程联立用未达定理的A、B两点坐标的关系,据向量共线的条件得椭圆中a,b,c的关系,从而求得椭圆的离心率.
解答 解:设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,则直线AB的方程为y=x-c,代入椭圆方程的$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,
化简得(a2+b2)x2-2a2cx+a2c2-a2b2=0.
令A(x1,y1),B(x2,y2),
则x1+x2=$\frac{2{a}^{2}c}{{a}^{2}+{b}^{2}}$,x1x2=$\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$,
∵$\overrightarrow{OA}$+$\overrightarrow{OB}$=(x1+x2,y1+y2),与$\overrightarrow{a}$=(3,-1)共线
∴3(y1+y2)+(x1+x2)=0,又y1=x1-c,y2=x2-c,
∴3(x1+x2-2c)+(x1+x2)=0,
∴x1+x2=$\frac{3}{2}$c,
∴$\frac{2{a}^{2}c}{{a}^{2}+{b}^{2}}$=$\frac{3}{2}$c
∴a2=3b2.
∴c=$\sqrt{{a}^{2}-{b}^{2}}$=a,
故离心率e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$.
故答案为:$\frac{\sqrt{6}}{3}$.
点评 考查向量共线为圆锥曲线提供已知条件;处理直线与圆锥曲线位置关系常用的方法是直线与圆锥曲线方程联立用韦达定理.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
13.若椭圆的长轴长、短轴长、焦距组成一个等差数列,则该椭圆的离心率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
15.方程mx2+ny2=1不可能表示的曲线为( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
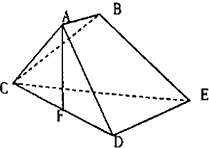 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.