题目内容
20．化简：$\frac{{x}^{2}+3x+9}{{x}^{3}-27}$+$\frac{6x}{9x-{x}^{2}}$-$\frac{x-1}{6+2x}$．分析 根据立方差和，平方差公式，化简计算即可．
解答 解：$\frac{{x}^{2}+3x+9}{{x}^{3}-27}$+$\frac{6x}{9x-{x}^{3}}$-$\frac{x-1}{6+2x}$，
=$\frac{{x}^{2}+3x+9}{（x-3）（{x}^{2}+3x+9）}$-$\frac{6x}{x（x-3）（x+3）}$-$\frac{x-1}{2（x-3）}$，
=$\frac{1}{x-3}$-$\frac{6}{（x+3）（x-3）}$-$\frac{x-1}{2（x+3）}$，
=$\frac{2x+6-12-{x}^{2}+4x-3}{2（x+3）（x-3）}$，
=-$\frac{{x}^{2}-6x+9}{2（x+3）（x-3）}$，
=-$\frac{（x-3）^{2}}{2（x+3）（x-3）}$，
=$\frac{3-x}{2x+6}$．
点评 本题主要考查了分式的化简，掌握立方差公式是关键，a3-b3=（a-b）（a2+ab+b2），属于基础题．
练习册系列答案
相关题目
8．将函数f（x）=cos2x（x∈R）的图象沿向量$\overrightarrow{a}$平移后，所得曲线对应的函数在区间[$\frac{π}{3}$，$\frac{2π}{3}$]内单调递增，且在该区间的最大值为1，则向量$\overrightarrow{a}$可能是（ ）
| A． | （-$\frac{π}{6}$，$\frac{1}{2}$） | B． | （$\frac{π}{6}$，$\frac{1}{2}$） | C． | （$\frac{π}{3}$，$\frac{3}{2}$） | D． | （-$\frac{π}{3}$，$\frac{3}{2}$） |
13．若椭圆的长轴长、短轴长、焦距组成一个等差数列，则该椭圆的离心率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
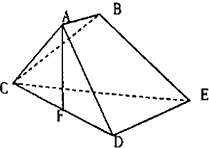已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，F为CD的中点．