题目内容
2.在△ABC中,已知a=4,b=x,A=60°,如果解该三角形有两解,则( )| A. | x>4 | B. | 0<x≤4 | C. | x≤$\frac{8\sqrt{3}}{3}$ | D. | 4<x<$\frac{8\sqrt{3}}{3}$ |
分析 结合图象可得如解该三角形有两解,则必须有:bsinA<a<b,代入已知即可得解.
解答 解:如图所示:
∵如果解该三角形有两解,则必须满足:CD<BC<AC,既有:bsinA<a<b,
∴xsin60°<4<x.
∴可解得:4<x<$\frac{8\sqrt{3}}{3}$.
故选:D.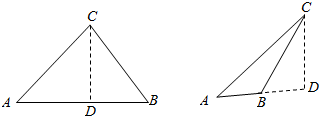
点评 本题主要考查了正弦定理在解三角形中的应用,属于基本知识的考查.

练习册系列答案
相关题目