题目内容
已知函数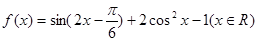
(1)求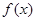 的单调递增区间;
的单调递增区间;
(2)在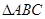 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为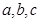 ,已知
,已知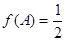 ,
,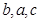 成等差数列,且
成等差数列,且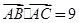 ,求边
,求边 的值.
的值.
(1)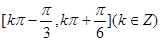 ;(2)
;(2)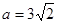 .
.
解析试题分析:(1)求三角函数的单调区间等问题,我们的目标很明确,就是要把函数化为 的形式,然后根据正弦函数的性质得出结论,本题中首先把
的形式,然后根据正弦函数的性质得出结论,本题中首先把
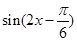 用两角差的正弦公式展开,再把
用两角差的正弦公式展开,再把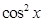 降幂把角化为
降幂把角化为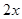 ,即化为同角的问题,再利用两角和或差的正弦公式,转化为一个三角函数;(2)已知
,即化为同角的问题,再利用两角和或差的正弦公式,转化为一个三角函数;(2)已知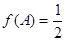 ,由(1)的结论应该很容易求出角A,
,由(1)的结论应该很容易求出角A,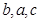 成等差数列得一个关系
成等差数列得一个关系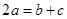 ,
,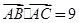 可以转化为
可以转化为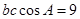 ,从而
,从而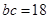 ,这是第二个关系,但其中有三个未知数
,这是第二个关系,但其中有三个未知数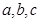 ,还需找一个关系式,
,还需找一个关系式,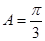 ,这里我们联想到余弦定理,正好找到第三个关系,从而联立方程组求出边
,这里我们联想到余弦定理,正好找到第三个关系,从而联立方程组求出边 .
.
试题解析:解:(1)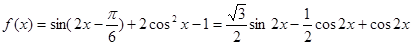
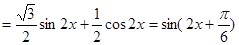
令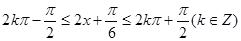
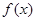 的单调递增区间为
的单调递增区间为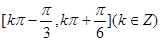
(2)由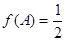 ,得
,得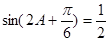
∵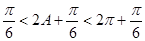 ,∴
,∴ ,∴
,∴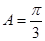
由b,a,c成等差数列得2a=b+c
∵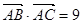 ,∴
,∴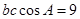 ,∴
,∴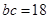
由余弦定理,得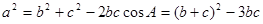
∴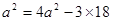 ,∴
,∴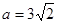
考点:(1)三角函数的单调性;(2)等差数列,向量的数量积定义,余弦定理.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 ,
, ,
, 三点.
三点. 和向量
和向量 的坐标;
的坐标; ,求
,求 的最小正周期;
的最小正周期; .
. 的最小正周期;
的最小正周期; 上的值域.
上的值域. ,
, 时,求
时,求 的值;
的值; 在
在 上的值域.
上的值域.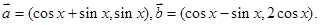
 与向量
与向量 不可能平行;
不可能平行; ,且
,且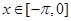 ,求
,求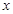 的值.
的值. 的一系列对应值如下表:
的一系列对应值如下表: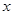








 的解析式;
的解析式; 中,
中, ,求
,求 的值.
的值.  分别是
分别是 的三个内角
的三个内角 的对边,
的对边, .
. 的大小;
的大小;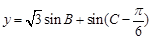 的值域.
的值域.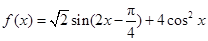 .
. 的最小正周期及最小值;
的最小正周期及最小值;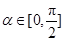 ,且
,且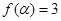 ,求
,求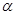 的值.
的值. ,其中角
,其中角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,
轴非负半轴重合, ,且
,且 .
.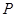 的坐标为
的坐标为 ,求
,求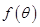 的值;
的值;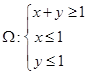 上的一个动点,试确定角
上的一个动点,试确定角