题目内容
15.已知函数f(x)=$\frac{-8}{ln2}ln(x+1)-\frac{4}{x+1}$.(1)求证:对任意的x∈[-$\frac{1}{2}$,+∞),函数f(x)的图象始终在x轴及其下方;
(2)若数列{an}的通项公式是an=1+$\frac{1}{n}$(n∈N*),前n项和是S,求证:Sn≥$\frac{2ln(n+1)}{ln2}$.
分析 (1)通过对f(x)=$\frac{-8}{ln2}ln(x+1)-\frac{4}{x+1}$求导可知函数f(x)在(-1,+∞)上单调递减,通过令f(x)=0,计算即得结论;
(2)利用数学归纳法证明,通过分析可知当n=k(k≥2)时只需证明$\frac{1+\frac{1}{k+1}}{ln(1+\frac{1}{k+1})}$>$\frac{2}{ln2}$,通过令g(x)=$\frac{1+x}{ln(1+x)}$,通过求导求出其单调区间,进而计算可得当n=k+1时命题成立.
解答 证明:(1)∵f(x)=$\frac{-8}{ln2}ln(x+1)-\frac{4}{x+1}$,
∴f′(x)=$\frac{-8}{(x+1)ln2}$+$\frac{4}{(x+1)^{2}}$=$\frac{-8(x+1)+4ln2}{(x+1)^{2}ln2}$,
令f′(x)=0可知x=$\frac{-2+ln2}{2}$<-$\frac{1}{2}$,
∴函数f(x)在($\frac{-2+ln2}{2}$,+∞)上单调递减,
令f(x)=$\frac{-8}{ln2}ln(x+1)-\frac{4}{x+1}$=0,解得:x=-$\frac{1}{2}$,
∴当x∈[-$\frac{1}{2}$,+∞)时,f(x)≤f(-$\frac{1}{2}$)=0,
于是对任意的x∈[-$\frac{1}{2}$,+∞),函数f(x)的图象始终在x轴及其下方;
(2)①当n=1时,1+$\frac{1}{1}$≥$\frac{2ln(1+1)}{ln2}$=2,即命题成立;
②假设当n=k(k≥2)时,Sk≥$\frac{2ln(k+1)}{ln2}$,
∴Sk+1+$\frac{1}{k+1}$≥$\frac{2ln(k+1)}{ln2}$+1+$\frac{1}{k+1}$,
下面证明:$\frac{2ln(k+1)}{ln2}$+1+$\frac{1}{k+1}$>$\frac{2ln(k+2)}{ln2}$,
即证:1+$\frac{1}{k+1}$>$\frac{2ln(1+\frac{1}{k+1})}{ln2}$,
即证:$\frac{1+\frac{1}{k+1}}{ln(1+\frac{1}{k+1})}$>$\frac{2}{ln2}$,
令g(x)=$\frac{1+x}{ln(1+x)}$,则g′(x)=$\frac{ln(1+x)-1}{[ln(1+x)]^{2}}$,
令g′(x)<0,得:-1<x<e-1,
∴当-1<x<e-1时,g(x)单调递减,
∵0<$\frac{1}{k+1}$≤$\frac{1}{2}$<1,
∴g($\frac{1}{k+1}$)>g(1),即$\frac{1+\frac{1}{k+1}}{ln(1+\frac{1}{k+1})}$>$\frac{2}{ln2}$,
即当n=k+1时,命题成立;
由①②可知:Sn≥$\frac{2ln(n+1)}{ln2}$.
点评 本题考查数列的求和,考查利用导数研究函数的单调性,考查运算求解能力,注意解题方法的积累,属于难题.

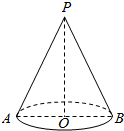 如图所示,圆锥的母线长l,轴截面PAB内,∠PAO=60°,
如图所示,圆锥的母线长l,轴截面PAB内,∠PAO=60°,
 如图,圆心在原点,半径为R的圆交x轴正半轴于点A,P、Q是圆上的两个动点,它们同时从点A出发沿圆周做匀速运动.点P逆时针方向每秒转$\frac{π}{3}$,点Q顺时针方向每秒转$\frac{π}{6}$,试求它们出发后第五次相遇时的位置及各自走过的弧长.
如图,圆心在原点,半径为R的圆交x轴正半轴于点A,P、Q是圆上的两个动点,它们同时从点A出发沿圆周做匀速运动.点P逆时针方向每秒转$\frac{π}{3}$,点Q顺时针方向每秒转$\frac{π}{6}$,试求它们出发后第五次相遇时的位置及各自走过的弧长.