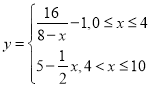题目内容
【题目】等腰三角形的周长是18，底边长y是一腰长x的函数，则（ ）
A.y＝9－x（0＜x≤9）
B.y＝9－x（0＜x＜9）
C.y＝18－2x（4．5≤x≤9）
D.y＝18－2x（4．5＜x＜9）
【答案】D
【解析】根据等腰三角形的周长公式列出函数解析式．
∵2x＋y＝18，∴y＝18－2x，则18－2x＞0，∴x＜9．由构成三角形的条件（两边之和大于第三边）可知2x＞18－2x，得x＞4．5，
∴函数的定义域为{x|4．5＜x＜9}.
故答案为:D.
实际问题中,根据等腰三角形的周长公式列出函数解析式,要注意函数的定义域.
练习册系列答案
相关题目
【题目】某单位共有10名员工，他们某年的收入如下表：
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪（万元） | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
（1）从该单位中任取2人，此2人中年薪收入高于5万的人数记为
，求
的分布列和期望；
（2）已知员工年薪收入
与工作所限
成正相关关系，某员工工作第一年至第四年的年薪如下表：
工作年限 | 1 | 2 | 3 | 4 |
年薪（万元） | 3.0 | 4.2 | 5.6 | 7.2 |
预测该员工第五年的年薪为多少？
附：线性回归方程
中系数计算公式和参考数据分别为：
，
，其中
为样本均值，
，
，（
）
