题目内容
15.求下列函数的值域(其中(1)和(4)请画出函数的图象)(1)f(x)=$\frac{1}{x+3}$;
(2)f(x)=$\frac{1}{{x}^{2}+3}$+3;
(3)f(x)=2x2-4x+3(-1<x<4);
(4)f(x)=|x+1|+$\sqrt{(x-2)^{2}}$;
(5)f(x)=2x2-4x+3(-1<x<a).
分析 (1)可认为f(x)的图象是由y=$\frac{1}{x}$的图象向左平移3个单位得到,画出图象,根据图象即可得出f(x)的值域;
(2)根据x2+3≥3求出$\frac{1}{{x}^{2}+3}$的范围,从而求出f(x)的范围,即f(x)的值域;
(3)配方,通过观察即可得到f(x)的取值范围,也即得到f(x)的值域;
(4)开平方得到$f(x)=|x+1|+|x-2|=\left\{\begin{array}{l}{-2x+1}&{x≤-1}\\{3}&{-1<x<2}\\{2x-1}&{x≥2}\end{array}\right.$,在每段上的图象为直线,画出图象,根据图象即可得出该函数的值域;
(5)配方得到f(x)=2(x-1)2+1,讨论a和区间(-1,3)的关系:a≤-1,-1<a<3,和a≥3,在每种情况下根据二次函数f(x)的单调性或取得顶点的情况及比较两端点值从而得出函数f(x)的值域.
解答 解:(1)画出f(x)的图象如下: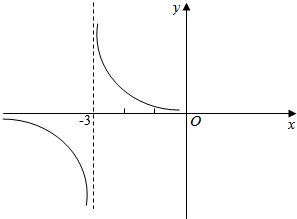
$\frac{1}{x+3}≠0$;
∴该函数的值域为{f(x)|f(x)≠0};
(2)x2+3≥3;
∴$0<\frac{1}{{x}^{2}+3}≤\frac{1}{3}$;
∴$3<f(x)≤\frac{10}{3}$;
∴原函数的值域为:$(3,\frac{10}{3}]$;
(3)f(x)=2(x-1)2+1≥1;
f(4)>f(-1),f(4)=19;
∴原函数的值域为[1,19);
(4)f(x)=|x+1|+|x-2|=$\left\{\begin{array}{l}{-2x+1}&{x≤-1}\\{3}&{-1<x<2}\\{2x-1}&{x≥2}\end{array}\right.$;
∴函数的图象如下: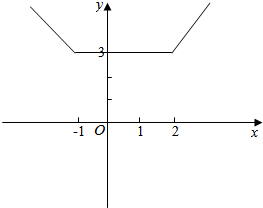 根据图象可看出该函数的值域为[3,+∞);
根据图象可看出该函数的值域为[3,+∞);
(5)f(x)=2(x-1)2+1;
①若-1<a≤1,则f(x)在(-1,a)上单调递减;
∴f(x)∈(f(a),f(-1))=(2(a-1)2+1,9);
∴f(x)的值域为:(2(a-1)2+1,9);
②1<a<3,则f(x)≥f(1)=1;
f(-1)=f(3);
∴f(x)的值域为:[1,9);
③若a≥3,f(x)≥1,且f(a)≥f(-1);
∴f(x)的值域为[1,2(a-1)2+1).
点评 考查平移变换的变换过程,掌握反比例函数的图象,根据不等式的性质求函数值域,处理含绝对值函数的方法:去绝对值号,以及根据函数图象求函数值域的方法,根据二次函数的单调性或取得顶点情况,及比较端点值的方法求函数的值域.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | {x|x≤3} | B. | {x|(x-1)(x+2)=0} | C. | {1,2,3,…} | D. | {x|-1≤x≤2} |
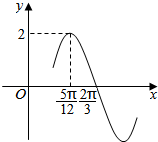 已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )| A. | [-$\frac{7π}{12}$,$\frac{5π}{12}$] | B. | [-$\frac{7π}{12}$,-$\frac{π}{12}$] | C. | [-$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{π}{12}$,$\frac{5π}{12}$] |