题目内容
17. 已知二面角α-l-β为锐角,A∈a,A到平面β的距离AH=2$\sqrt{3}$,点A到棱的距离为AB=4,则二面角α-l-β的大小为( )
已知二面角α-l-β为锐角,A∈a,A到平面β的距离AH=2$\sqrt{3}$,点A到棱的距离为AB=4,则二面角α-l-β的大小为( )| A. | 15° | B. | 50° | C. | 60° | D. | 45° |
分析 连接BH,便可说明∠ABH为二面角α-l-β的平面角,从而在Rt△ABH中可求出sin∠ABH,从而求得∠ABH.
解答 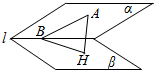 解:如图,连接BH;
解:如图,连接BH;
AH⊥β,l?β;
∴AH⊥l,又AB⊥l,AB∩AH=A;
∴l⊥平面ABH;
∴l⊥BH;
∴∠ABH为二面角α-l-β的平面角;
在Rt△ABH中,AH=$2\sqrt{3}$,AB=4,∠AHB=90°,∴$sin∠ABH=\frac{AH}{AB}=\frac{\sqrt{3}}{2}$;
∴∠ABH=60°.
故选:C.
点评 考查平面上一点到另一平面距离的概念,空间一点到一直线的距离的概念,线面垂直的性质,线面垂直的判定定理,以及二面角的平面角的定义及求法,本题是将二面角平面角放在直角三角形中求解.

练习册系列答案
相关题目
8.已知Rt△ABC中,AB=AC=a,AD是斜边上的高,以AD为折痕使∠BDC成直角.则折后几何体中,∠BAC的度数为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
6.已知M是△ABC内一点,且$\overrightarrow{AB}•\overrightarrow{AC}=2\sqrt{3},∠BAC={30°}$,若△MBC,△MCA,△MAB的面积分别为$\frac{1}{2},x,y$,则xy的最大值是( )
| A. | $\frac{1}{14}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{20}$ |
 如图,已知AE⊥平面CDE,四边形ABCD为正方形,M,N分别是线段BE,DE的中点.
如图,已知AE⊥平面CDE,四边形ABCD为正方形,M,N分别是线段BE,DE的中点. 四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列
四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列