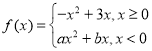题目内容
【题目】已知函数
（
为实数）．
（1）当
时，判断函数
的单调性，并用定义证明；
（2）根据的不同取值，讨论的奇偶性，并说明理由．
【答案】（1）定义域单调递增，证明见解析；（2）见解析
【解析】
（1）
时，
，设
，计算
得到答案.
（2）计算
，根据
和
之间的关系求得
.
（1）a＝0时，f（x）
，函数单调递增.
设x1＞x2，f（x1）﹣f（x2）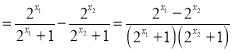
∵x1＞x2，∴2
2
0，f（x1）﹣f（x2）＞0，
∴f（x）在定义域单调递增
（2）f（﹣x）
，
①当a＝﹣1时，f（﹣x）＝f（x），即f（x）为偶函数；
②当a＝1时，f（﹣x）＝﹣f（x），即为奇函数；
③当则a≠1且a≠﹣1时，f（﹣x）≠﹣f（x）且f（﹣x）≠f（x），即非奇非偶函数．
综上所述：
时为偶函数；
时为奇函数；
且
时为非奇非偶函数.
练习册系列答案
阅读快车系列答案
相关题目
【题目】行了一次水平测试。用系统抽样的方法抽取了50名学生的数学成绩，准备进行分析和研究。经统计成绩的分组及各组的频数如下：
，2；
，3；
，10；
，15；
，12；
，8.
（Ⅰ）频率分布表
分组 | 频数 | 频率 |
| 2 | |
| 3 | |
| 10 | |
| 15 | |
| 12 | |
| 8 | |
合计 | 50 |
频率分布直方图为
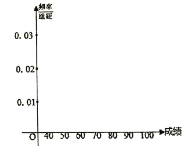
（Ⅰ）完成样本的频率分布表；画出频率分直方图；
（Ⅱ）估计成绩在85分以下的学生比例；
（Ⅲ）请你根据以上信息去估计样本的众数、中位数、平均数.（精确到0.01）
