��Ŀ����
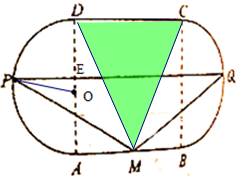
4�� ij���ٰ컨չ������һ��չ��ƽ��ͼ��ͼ��ʾ���м������DZ߳�Ϊ10��������ABCD����������ֱ�����AD��BCΪֱ���İ�Բ�������м仮��һ������������MPQ������MΪAB���е㣬PQ��AB�����мס������ֻ�չ�������ֻ��ļ۸�Ϊ2��Ԫ/ƽ���ף���������������MPQ�����ֻ��ļ۸�Ϊ4��Ԫ/ƽ���ף�������������
ij���ٰ컨չ������һ��չ��ƽ��ͼ��ͼ��ʾ���м������DZ߳�Ϊ10��������ABCD����������ֱ�����AD��BCΪֱ���İ�Բ�������м仮��һ������������MPQ������MΪAB���е㣬PQ��AB�����мס������ֻ�չ�������ֻ��ļ۸�Ϊ2��Ԫ/ƽ���ף���������������MPQ�����ֻ��ļ۸�Ϊ4��Ԫ/ƽ���ף���������������1����P��Q�ֱ������ڰ�Բ���е�ʱ�����չ���ܷ��ã���λ����Ԫ����
��2�����չ���ܷ��õ���Сֵ����λ����Ԫ��
���� ��1����P��Q�ֱ������ڰ�Բ���е�ʱ���ֱ�����������������������չ���ܷ��ã���λ����Ԫ����
��2���������ǻ�Ԫ��������ȡ��ֵ�ĵȼ��������ɵõ����ۣ�
���  �⣺��1����P��Q�ֱ������ڰ�Բ���е�ʱ��
�⣺��1����P��Q�ֱ������ڰ�Բ���е�ʱ��
PQ=20�ף�������PQM�ĸ�h=5�ף�
��������PQM�����S=$\frac{1}{2}��20��5=50$ƽ���ף�
����չ�������S=10��10+�С�52=100+25�С�100+78.5=178.5��
����������Ϊ178.5-50=128.5��
���Ӧ�ܷ���Ϊ2��50+128.5��4=614����Ԫ����
��2��Ҫʹ�ܷ�����С����ֻ��Ҫ����������MPQ��ɣ�
��PQ��AD��E����Բ��Բ��ΪO���뾶OD=OP=5��
���POE=�ȣ�0��x��$\frac{��}{2}$��
��OP=5��OE=OPcos��=5cos�ȣ�PE=OPsin��=5sin�ȣ�
����PMQ�ĸ�ΪAE=5+5cos�ȣ�
��PQ=2PE+10=10+10sin�ȣ�
���MPQ�����S=$\frac{1}{2}$��10+10sin�ȣ���5+cos�ȣ�
=��5+5cos�ȣ���5+sin�ȣ�
=25��1+cos�ȣ���1+sin�ȣ�
=25��1+sin��+cos��+sin��cos�ȣ���
��t=sin��+cos��=$\sqrt{2}$sin����+$\frac{��}{4}$����
��sin��cos��=$\frac{1}{2}$��t2-1����
��0��x��$\frac{��}{2}$��
��$\frac{��}{4}$�ܦ�+$\frac{��}{4}$��$\frac{3��}{2}$����-1��t��1��
������ȼ�ΪS=25[1+t+$\frac{1}{2}$��t2-1��]=$\frac{25}{2}$��t2+2t+1��=$\frac{25}{2}$��t+1��2��
��-1��t��1��
�൱t=1ʱ�����Sȡ�����ֵ����ʱPΪΪD�㣬���ֵΪS=$\frac{25}{2}$��1+1��2=$\frac{25}{2}$��4=50��
��������������S=50+��52=50+25��50+78.5=128.5��
���Ӧ�ķ���Ϊ2��50+128.5��4=614����Ԫ����
���� ������Ҫ���麯����Ӧ�����⣬�������Ǻ�����Ԫ���ǽ������Ĺؼ����ۺ��Խ�ǿ���ѶȽϴ�

 ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�| A�� | a��b��c | B�� | b��a��c | C�� | c��a��b | D�� | c��b��a |
| A�� | -3 | B�� | -$\sqrt{3}$ | C�� | $\sqrt{3}$ | D�� | 3 |