题目内容
3.某校高三年级本学期共进行了四次阶段考试,在每份数学试卷中,第Ⅰ卷共10道选择题,每小题得对的5分,答错得0分,学生甲、乙在四次考试中选择题答错的题目数如下所示:| 甲 | 3 | 2 | 0 | 1 |
| 乙 | 4 | 3 | 2 | 0 |
(2)记以甲每次考试答错的题目数为元素构成集合A,以乙每次考试答错的题目数为元素构成集合B,在直角坐标平面上有点P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,求满足k≥2的事件的概率.
分析 (Ⅰ)根据平均数的计算公式计算即可;
(Ⅱ)根据斜率公式,以及k≥2得到y≥2x-1,分别列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
解答 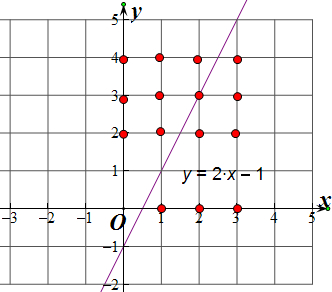 解:(1)答对题目$\overrightarrow{x}$=$\frac{1}{4}$(7+8+10+9)=8.5.
解:(1)答对题目$\overrightarrow{x}$=$\frac{1}{4}$(7+8+10+9)=8.5.
第Ⅰ卷的平均得分$\overline{x}$=8.5×5=42.5分,
(Ⅱ)∵P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,
∴k=$\frac{y+2}{x+1}$,
∵k≥2,
∴$\frac{y+2}{x+1}$≥2,即y≥2x-1,
∵记以甲每次考试答错的题目数为元素构成集合A=(3,2,0,1),以乙每次考试答错的题目数位元素构成集合B=(4,3,2,0),在直角坐标平面上有点P(x,y),其中x∈A,y∈B,
∴满足条件的基本事件有(3,4),(3,3),(3,2),(3,0),(2,4),(2,3),(2,2),(2,0),(0,4),(0,3),(0,2),(0,0),(1,4),(1,3),(1,2),(1,0),共16种基本事件,
其中满足y≥2x-1,由图可知有8种,
故满足k≥2的事件的概率为$\frac{8}{16}$=$\frac{1}{2}$.
点评 本题考查了平均数和古典概型的概率问题,根据题意得到y≥2x-1是关键,属于中档题.

练习册系列答案
相关题目
8.设x,y∈R且满足$\left\{\begin{array}{l}{x≥1}\\{x+y-6≤0}\\{y≥x}\end{array}\right.$,则z=x+2y的最小值等于( )
| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
15.已知a=cos100°,b=cos70°,c=sin40°,这三个数的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
12.已知tanα,tanβ是方程x2+3$\sqrt{3}$x+4=0的两根,则tan(α+β)等于( )
| A. | -3 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |