题目内容
【题目】如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O．沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED． 
（1）求证：BD⊥平面POA；
（2）设点Q满足 
，试探究：当PB取得最小值时，直线OQ与平面PBD所成角的大小是否一定大于 
？并说明理由．
【答案】
（1）证明：∵菱形ABCD的对角线互相垂直，∴BD⊥AC，∴BD⊥AO，
∵EF⊥AC，∴PO⊥EF．
∵平面PEF⊥平面ABFED，平面PEF∩平面ABFED=EF，且PO平面PEF，
∴PO⊥平面ABFED，
∵BD平面ABFED，∴PO⊥BD．
∵AO∩PO=O，∴BD⊥平面POA
（2）解：如图，以O为原点，建立空间直角坐标系O﹣xyz．
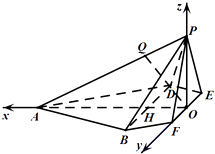
设AO∩BD=H．因为∠DAB=60°，所以△BDC为等边三角形，
故BD=4， 
．
又设PO=x，则 
， 
，
所以O（0，0，0），P（0，0，x）， 
， 
，
故 
，
所以 
，
当 
时， 
．此时 
设点Q的坐标为（a，0，c），由（1）知， 
，则 
， 
， ， 
．
∴ 
， 
，
∵ 
，∴ 
．
∴ 
，∴ 
．
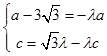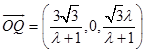设平面PBD的法向量为 
，则 
．
∵ 
， 
，∴ 
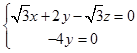
取x=1，解得：y=0，z=1，所以 
．
设直线OQ与平面E所成的角θ，
∴ 
= 
．
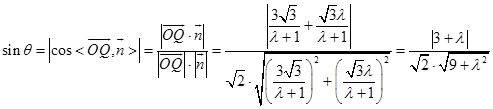又∵λ＞0∴ 
．∵ 
，∴ 
．
因此直线OQ与平面E所成的角大于 
，即结论成立．
【解析】（1）利用菱形ABCD的对角线互相垂直证明BD⊥AO，证明PO⊥平面ABFED，可得PO⊥BD，利用线面垂直的判定，可得 BD⊥平面POA；（2）建立空间直角坐标系O﹣xyz，设PO=x，求出 时， ，此时 ，进一步求点Q的坐标，求出平面PBD的法向量 ，利用向量的夹角公式，可证直线OQ与平面E所成的角大于 ．
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想，以及对空间角的异面直线所成的角的理解，了解已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则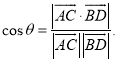
．
