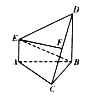
题目内容
【题目】已知椭圆:![]() ,点
,点![]() .
.
(1)设![]() 是椭圆
是椭圆![]() 上任意的一点,
上任意的一点,![]() 是点
是点![]() 关于坐标原点的对称点,记
关于坐标原点的对称点,记![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)已知点![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上在第一象限内的点,记
上在第一象限内的点,记![]() 为经过原点与点
为经过原点与点![]() 的直线,
的直线,![]() 为
为![]() 截直线
截直线![]() 所得的线段长,试将
所得的线段长,试将![]() 表示成直线
表示成直线![]() 的斜率
的斜率![]() 的函数.
的函数.
【答案】(1)![]() ;(2)
;(2)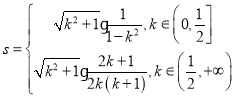 .
.
【解析】
试题分析:(1)设![]() 的坐标为
的坐标为![]() ,则
,则![]() 的坐标为
的坐标为![]() ,先求出
,先求出![]() 和
和![]() ,然后运用向量数量积的坐标运算能够求出
,然后运用向量数量积的坐标运算能够求出![]() 的取值范围;(2)根据
的取值范围;(2)根据![]() 为双曲线
为双曲线![]() 上第一象限内的点,可知直线
上第一象限内的点,可知直线![]() 的斜率
的斜率![]() ,再由题设条件根据
,再由题设条件根据![]() 的不同取值范围试将
的不同取值范围试将![]() 表示为直线
表示为直线![]() 的斜率
的斜率![]() 的函数.
的函数.
试题解析:(1)设![]() ,则
,则![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() .
.
(2)因为![]() 是椭圆
是椭圆![]() 上在第一象限内的点,则
上在第一象限内的点,则![]() 的斜率
的斜率![]() ,且
,且![]() .
.
当![]() 时,
时,![]() 截直线
截直线![]() 所得的线段的两个端点分别是直线
所得的线段的两个端点分别是直线![]() 与直线
与直线![]() 的交点
的交点![]() ,由已知
,由已知![]() ,
,![]() ,
,
联立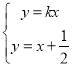 解得
解得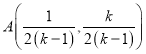 ,联立
,联立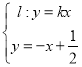 解得
解得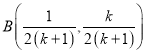 ,
,
于是![]() ;
;
当![]() 时,
时,![]() 截直线
截直线![]() 所得的线段的两个端点分别是直线
所得的线段的两个端点分别是直线![]() 与直线
与直线![]() 的交点
的交点![]() ,由已知
,由已知![]() ,
,
联立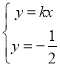 解得
解得![]() ,
,
于是![]() .
.
综上所述,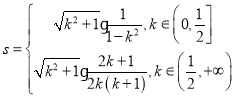 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目