题目内容
【题目】如图所示,在三棱锥S—ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=3a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】作AD⊥CB交CB的延长线于点D,连接SD,如图所示.
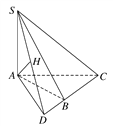
∵SA⊥平面ABC,BC平面ABC,
∴SA⊥BC.又BC⊥AD,SA∩AD=A,SA平面SAD,AD平面SAD,
∴BC⊥平面SAD,又BC平面SBC,
∴平面SBC⊥平面SAD,且平面SBC∩平面SAD=SD.在平面SAD内,过点A作AH⊥SD于点H,则AH⊥平面SBC,AH的长即为点A到平面SBC的距离.
在Rt△SAD中,SA=3a,AD=AB·sin 60°=![]() a.由
a.由![]()
得AH=![]() ,即点A到平面SBC的距离为
,即点A到平面SBC的距离为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目