题目内容
【题目】设函数![]() .
.
(Ⅰ)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 范围;
范围;
(Ⅱ)方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:1)求出函数的导数,求出函数的单调区间,求出函数的最大值,从而求出k的范围即可;(2)lnx+x=0时,不合题意,当lnx+x≠0时,m=![]() 有唯一解,此时x>x0,记h(x)=
有唯一解,此时x>x0,记h(x)=![]() ,根据函数的单调性求出m的值即可.
,根据函数的单调性求出m的值即可.
解析:
(1)a=2时,f(x)=lnx﹣x2+x,
f(x)的定义域是(0,+∞),
f′(x)=![]() ﹣2x+1,
﹣2x+1,
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
故f(x)在(0,1)递增,在(1,+∞)递减,
故f(x)max=f(1)=0,
若f(x)≤k恒成立,
则k≥0;
(2)方程mf(x)=(1﹣![]() )x2有唯一实数解,
)x2有唯一实数解,
即m(lnx+x)=x2有唯一实数解,
当lnx+x=0时,显然不成立,设lnx+x=0的根为x0∈(![]() ,1)
,1)
当lnx+x≠0时,m=![]() 有唯一解,此时x>x0
有唯一解,此时x>x0
记h(x)=![]() ,
,
h′(x)=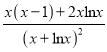 ,
,
当x∈(0,1)时,x(x﹣1)<0,2xlnx<0,h′(x)<0,
当x∈(1,+∞)时,x(x﹣1)>0,2xlnx>0,h'(x)>0,
∴h(x)在(x0,1)上递减,(1,+∞)上递增.
∴h(x)min=h(1)=1,
当x∈(x0,1)时,h(x)∈(1,+∞),
当x∈(1,+∞)时,h(x)∈(1,+∞),
要使m=![]() 有唯一解,应有m=h(1)=1,
有唯一解,应有m=h(1)=1,
∴m=1.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目