题目内容
【题目】已知抛物线![]() 的标准方程为
的标准方程为![]() ,
, ![]() 为抛物线
为抛物线![]() 上一动点,
上一动点, ![]() (
(![]() )为其对称轴上一点,直线
)为其对称轴上一点,直线![]() 与抛物线
与抛物线![]() 的另一个交点为
的另一个交点为![]() .当
.当![]() 为抛物线
为抛物线![]() 的焦点且直线
的焦点且直线![]() 与其对称轴垂直时,
与其对称轴垂直时, ![]() 的面积为18.
的面积为18.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)记![]() ,若
,若![]() 值与
值与![]() 点位置无关,则称此时的点
点位置无关,则称此时的点![]() 为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
【答案】(1)抛物线![]() 的标准方程为
的标准方程为![]() ;(2)
;(2)![]() 时,
时, ![]() 与
与![]() 无关.
无关.
【解析】试题分析:(1)由已知![]() 为通径,因此
为通径,因此![]() ,由
,由![]() 可求得
可求得![]() ;(2)定点问题处理,设
;(2)定点问题处理,设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,代入抛物线方程,由韦达定理得
,代入抛物线方程,由韦达定理得![]() ,计算
,计算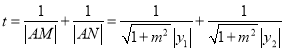
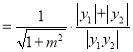 ,按
,按![]() 和
和![]() 分类后讨论可得
分类后讨论可得![]() 取特定值时
取特定值时![]() 与
与![]() 无关,即
无关,即![]() 为稳定点.
为稳定点.
试题解析:(1)由题意, ![]() ,∴
,∴![]() ,
,
抛物线![]() 的标准方程为
的标准方程为![]()
(2)设![]() ,
,
设直线![]() 的方程为
的方程为![]() ,联立
,联立![]() 得
得![]() ,
,
∴![]() ,
, ![]() ,
,
由对称性,不妨设![]() ,
,
①![]() 时,∵
时,∵![]() ,∴
,∴![]() 同号,
同号,
又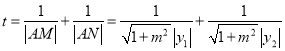 ,
,
∴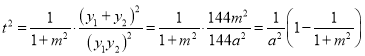 ,
,
不论![]() 取何值,
取何值, ![]() 均与
均与![]() 有关,即
有关,即![]() ,
, ![]() 不是“稳定点”;
不是“稳定点”;
②![]() 时,∵
时,∵![]() ,∴
,∴![]() 异号.
异号.
又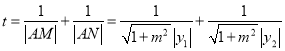 ,
,
∴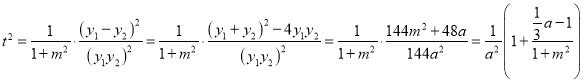 ,
,
∴仅当![]() ,即
,即![]() 时,
时, ![]() 与
与![]() 无关,稳定点为
无关,稳定点为![]()

练习册系列答案
相关题目