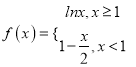题目内容
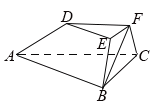
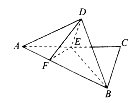
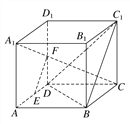
【题目】如图，在正方体ABCD－A1B1C1D1中，E，F分别是AD，DD1的中点．
求证：(1)EF∥平面C1BD；
(2)A1C⊥平面C1BD.
【答案】(1)见解析；(2)见解析.
【解析】试题分析：（1）利用三角形中位线性质得EF∥AD1。即得EF∥BC1，再根据线面平行判定定理得结论（2）由正方体性质得AA1⊥BD，再根据正方形性质得AC⊥BD，可由线面垂直判定定理得BD⊥平面AA1C，即得A1C⊥BD.类似可得A1C⊥BC1，即证得A1C⊥平面C1BD.
试题解析：证明 (1)如图，连接AD1，
∵E，F分别是AD和DD1的中点，
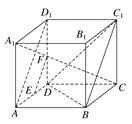
∴EF∥AD1.
在正方体ABCD－A1B1C1D1中，AB∥D1C1，AB＝D1C1，∴四边形ABC1D1为平行四边形，
即有AD1∥BC1，∴EF∥BC1.
又EF平面C1BD，BC1平面C1BD，
∴EF∥平面C1BD.
(2)如图，连接AC，则AC⊥BD.
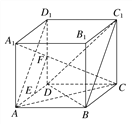
∵在正方体ABCD－A1B1C1D1中，AA1⊥平面ABCD，BD平面ABCD，
∴AA1⊥BD.
又AA1∩AC＝A，AA1平面AA1C，AC平面AA1C，
∴BD⊥平面AA1C，A1C平面AA1C，
∴A1C⊥BD.
同理可证A1C⊥BC1.
又BD∩BC1＝B，BD平面C1BD，BC1平面C1BD，
∴A1C⊥平面C1BD.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行，需转化为证明线线平行.
(2)证明线面垂直，需转化为证明线线垂直.
(3)证明线线垂直，需转化为证明线面垂直.
【题目】已知函数f(x)＝x2＋ex－
(x＜0)与g(x)＝x2＋ln(x＋a)图象上存在关于y轴对称的点，则a的取值范围是( )
A. (－∞，
) B. (－∞，
)
C. (－
， 
) D. (－
， 
)
