题目内容
【题目】已知m>0,p:(x+2)(x-6)≤0,q:2-m≤x≤2+m.
(1)若p是q成立的必要不充分条件,求实数m的取值范围;
(2)若![]() 是
是![]() 成立的充分不必要条件,求实数m的取值范围.
成立的充分不必要条件,求实数m的取值范围.
【答案】(1) (0,4)(2) 实数m的取值范围为(4,+∞).
【解析】试题分析:(1)先解不等式得p,再由p是q成立的必要不充分条件得![]() ,最后根据集合包含关系以及数轴求实数m的取值范围.(2)先根据原命题与逆否命题等价得p是q的充分不必要条件,即得
,最后根据集合包含关系以及数轴求实数m的取值范围.(2)先根据原命题与逆否命题等价得p是q的充分不必要条件,即得![]() ,最后根据集合包含关系以及数轴求实数m的取值范围.
,最后根据集合包含关系以及数轴求实数m的取值范围.
试题解析:p:-2≤x≤6,
(1)∵p是q的必要不充分条件,∴[2-m,2+m] ![]() [-2,6],∴
[-2,6],∴![]() ∴m≤4.
∴m≤4.
∵当m=4时,不符合条件,∵m>0,∴m的取值范围是(0,4).
(2)∵![]() 是
是![]() 的充分不必要条件,∴p是q的充分不必要条件,
的充分不必要条件,∴p是q的充分不必要条件,
∴[-2,6]是[2-m,2+m]的真子集.
∴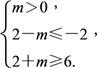 得m≥4,当m=4时,不符合条件.∴实数m的取值范围为(4,+∞).
得m≥4,当m=4时,不符合条件.∴实数m的取值范围为(4,+∞).

练习册系列答案
相关题目