题目内容
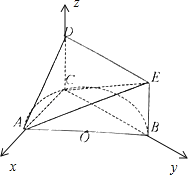
【题目】如图,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
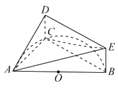
(1)证明:平面ADE⊥平面ACD;
(2)当C点为半圆的中点时,求二面角D﹣AE﹣B的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由BC⊥AC,BC⊥CD得BC⊥平面ACD,证明四边形DCBE是平行四边形得DE∥BC,故而DE![]() 平面ACD,从而得证面面垂直;
平面ACD,从而得证面面垂直;
(2)建立空间坐标系,求出两半平面的法向量,计算法向量的夹角得出二面角的大小.
(1)证明:∵AB是圆O的直径,∴AC⊥BC,
∵DC⊥平面ABC,BC平面ABC,
∴DC⊥BC,又DC∩AC=C,
∴BC⊥平面ACD,
∵DC∥EB,DC=EB,
∴四边形DCBE是平行四边形,∴DE∥BC,
∴DE⊥平面ACD,
又DE平面ADE,
∴平面ACD⊥平面ADE.
(2)当C点为半圆的中点时,AC=BC=2![]() ,
,
以C为原点,以CA,CB,CD为坐标轴建立空间坐标系如图所示:
则D(0,0,1),E(0,2![]() ,1),A(2
,1),A(2![]() ,0,0),B(0,2
,0,0),B(0,2![]() ,0),
,0),
∴![]() (﹣2
(﹣2![]() ,2
,2![]() ,0),
,0),![]() (0,0,1),
(0,0,1),![]() (0,2
(0,2![]() ,0),
,0),![]() (2
(2![]() ,0,﹣1),
,0,﹣1),
设平面DAE的法向量为![]() (x1,y1,z1),平面ABE的法向量为
(x1,y1,z1),平面ABE的法向量为![]() (x2,y2,z2),
(x2,y2,z2),
则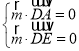 ,
,,即
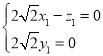 ,
,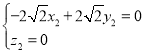 ,
,
令x1=1得![]() (1,0,2
(1,0,2![]() ),令x2=1得
),令x2=1得![]() (1,1,0).
(1,1,0).
∴cos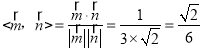 .
.
∵二面角D﹣AE﹣B是钝二面角,
∴二面角D﹣AE﹣B的余弦值为![]() .
.

 全能测控期末小状元系列答案
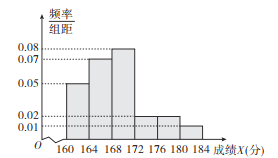
全能测控期末小状元系列答案【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成如下的频率分布直方图;

(2)组委会决定在5名(其中第3组2名,第4组2名,第5组1名)选手中随机抽取2名选接受![]() 考官进行面试,求第4组至少有1名选手被考官
考官进行面试,求第4组至少有1名选手被考官![]() 面试的概率.
面试的概率.