题目内容
6.已知函数f(x)=ax3+bx2-3x,(a,b∈R)在点x=-1处取得极大值为2,求:(1)函数f(x)的解析式;
(2)函数f(x)在区间[-2,2]的最值.
分析 (1)先求出函数f(x)的导数,得到不等式组,求出a,b的值,从而求出函数的解析式;
(2)先求出函数的导数,解关于导函数的不等式,得到函数的单调区间,从而求出函数的最值.
解答 解:(1)f′(x)=3ax2+2bx-3,
依题意得:f(-1)=2,f′(-1)=0,
即$\left\{\begin{array}{l}{3a-2b-3=0}\\{-a+b+3=2}\end{array}\right.$,
解得a=1,b=0,
∴f(x)=x3-3x;
(2)由(1)得:f(x)=x3-3x,f′(x)=3x2-3,
令f′(x)>0,解得:x>1或x<-1,
令f′(x)<0,解得:-1<x<1,
∴f(x)在[-2,-1),(1,2]递增,在(-1,1)递减,
∴f(x)极大值=f(-1)=-1+3=2,
f(x)极小值=f(1)=1-3=-2,
而f(-2)=-8+6=-2,f(2)=8-6=2,
∴f(x)在[-2,2]上的最小值是-2,最大值是2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知F1,F2是距离为6的两个定点,动点M满足|MF1|+|MF2|=6,则M点的轨迹是( )
| A. | 椭圆 | B. | 直线 | C. | 线段 | D. | 圆 |
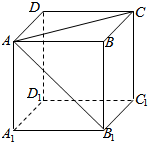 在如图所示的正方体ABCD-A1B1C1D1中,求:
在如图所示的正方体ABCD-A1B1C1D1中,求: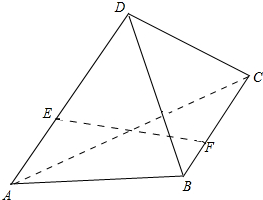 如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.
如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.