题目内容
15.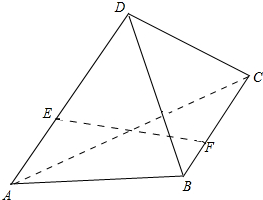 如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.
如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.
分析 可作EG∥AB,并交BD于G,并连接GF,根据条件即可说明EG∥AB,GF∥CD,从而便得到异面直线AB与CD所成角为∠EGF或其补角,并且可以根据比例关系求出EG,GF,这样在△EFG中根据余弦定理即可得出cos∠EGF,从而得出该角,这样便能得到AB和CD所成角.
解答 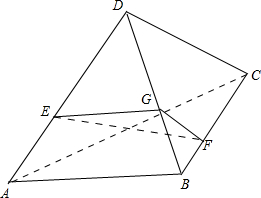 解:如图,作EG∥AB,交BD于G,并连接GF,则:
解:如图,作EG∥AB,交BD于G,并连接GF,则:
∵$\frac{AE}{ED}=\frac{1}{2}$;
∴$\frac{BG}{GD}=\frac{1}{2}$;
又$\frac{BF}{FC}=\frac{1}{2}$;
∴GF∥CD;
∴∠EGF或其补角便是异面直线AB和CD所成的角;
根据前面,$\frac{EG}{AB}=\frac{DE}{AD}=\frac{2}{3}$,$\frac{GF}{CD}=\frac{BF}{BC}=\frac{1}{3}$,且AB=CD=3;
∴EG=2,GF=1,又EF=$\sqrt{7}$;
∴在△EFG中,由余弦定理得:cos$∠EGF=\frac{E{G}^{2}+G{F}^{2}-E{F}^{2}}{2EG•GF}=\frac{4+1-7}{4}=-\frac{1}{2}$;
∴∠EGF=120°;
∴AB和CD所成的角为60°.
点评 考查平行线分线段成比例定理,平行线的判定,以及异面直线所成角的定义及求法,余弦定理求三角形的内角.

练习册系列答案
相关题目
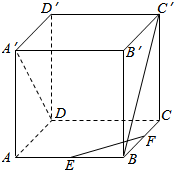 如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求:
如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求: