题目内容
16.抛物线C:y=x2在点P处的切线l分别交x轴、y轴于不同的两点A、B,$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{MB}$.当点P在C上移动时,点M的轨迹为D.(1)求曲线D的方程;
(2)设直线l与曲线D的另一个交点为N,曲线D在点M、N处的切线分别为m、n,直线m、n相交于点Q.证明:PQ平行于x轴.
分析 (1)求导函数,可得直线l方程,确定A,B的坐标,利用,$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{MB}$,即可求出曲线D的方程;
(2)求出直线m、n的方程,确定点Q纵坐标为x02,即可证明PQ平行于x轴.
解答 解:(1)对y=x2,求导,得y′=2x.
设点P(x0,x02)(x0≠0),则直线l方程为y-x02=2x0(x-x0),即y=2x0x-x02,
在l方程中分别令y=0,x=0,得A($\frac{1}{2}$x0,0)、B(0,-x02).
设M(x,y),
∵$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{MB}$
∴(x-$\frac{1}{2}$x0,y)=$\frac{1}{2}$(-x,-x02-y).
由此得x0=3x,x02=-3y,
消去x0,得曲线D的方程为y=-3x2(x≠0).
(2)将y=-3x2代入直线l方程,并整理得3x2+2x0x-x02=0,
由(1)知,M($\frac{{x}_{0}}{3}$,-$\frac{{{x}_{0}}^{2}}{3}$),设N(x1,-3x12),则$\frac{{x}_{0}}{3}$•x1=-$\frac{{{x}_{0}}^{2}}{3}$,
∴x1=-x0.
对y=-3x2求导,得y′=-6x,
于是直线m、n的方程分别为y+$\frac{{{x}_{0}}^{2}}{3}$=-2x0(x-$\frac{{x}_{0}}{3}$)和y+3x02=6x0(x+x0),
即y=-2x0x+$\frac{{{x}_{0}}^{2}}{3}$和y=6x0x+3x02,
由此得点Q纵坐标为x02,故PQ平行于x轴.
点评 本题考查轨迹方程,考查直线与抛物线的位置关系,考查导数知识的运用,知识综合性强.

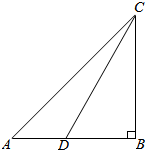 如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.
如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.