题目内容
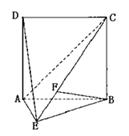
已知三棱锥P—ABC中,PC⊥底面ABC,AB=BC,
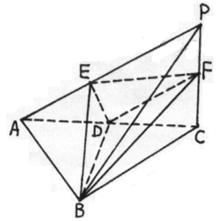
D、F分别为AC、PC的中点,DE⊥AP于E.
(1)求证:AP⊥平面BDE;
(2)求证:平面BDE⊥平面BDF;
(3)若AE∶EP=1∶2,求截面BEF分三棱锥
P—ABC所成两部分的体积比.

D、F分别为AC、PC的中点,DE⊥AP于E.
(1)求证:AP⊥平面BDE;
(2)求证:平面BDE⊥平面BDF;
(3)若AE∶EP=1∶2,求截面BEF分三棱锥
P—ABC所成两部分的体积比.
(Ⅰ)证明见解析(Ⅱ)证明见解析(Ⅲ)两部分体积的比为1∶2或2∶1
(1)∵PC⊥底面ABC,BD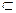 平面ABC,∴PC⊥BD.
平面ABC,∴PC⊥BD.
由AB=BC,D为AC的中点,得BD⊥AC.又PC∩AC=C,∴BD⊥平面PAC.又PA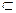 平面、PAC,∴BD⊥PA.由已知DE⊥PA,DE∩BD=D,∴AP⊥平面BDE.
平面、PAC,∴BD⊥PA.由已知DE⊥PA,DE∩BD=D,∴AP⊥平面BDE.
(2)由BD⊥平面PAC,DE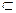 平面PAC,得BD⊥DE.由D、F分别为AC、PC的中点,得DF//AP.
平面PAC,得BD⊥DE.由D、F分别为AC、PC的中点,得DF//AP.
由已知,DE⊥AP,∴DE⊥DF. BD∩DF=D,∴DE⊥平面BDF.
又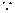 DE
DE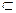 平面BDE,∴平面BDE⊥平面BDF.
平面BDE,∴平面BDE⊥平面BDF.
(3)设点E和点A到平面PBC的距离分别为h1和h2.则
h1∶h2=EP∶AP=2∶3,
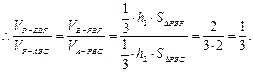
故截面BEF分三棱锥P—ABC所成两部分体积的比为1∶2或2∶1
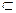 平面ABC,∴PC⊥BD.
平面ABC,∴PC⊥BD.由AB=BC,D为AC的中点,得BD⊥AC.又PC∩AC=C,∴BD⊥平面PAC.又PA
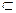 平面、PAC,∴BD⊥PA.由已知DE⊥PA,DE∩BD=D,∴AP⊥平面BDE.
平面、PAC,∴BD⊥PA.由已知DE⊥PA,DE∩BD=D,∴AP⊥平面BDE.(2)由BD⊥平面PAC,DE
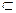 平面PAC,得BD⊥DE.由D、F分别为AC、PC的中点,得DF//AP.
平面PAC,得BD⊥DE.由D、F分别为AC、PC的中点,得DF//AP.由已知,DE⊥AP,∴DE⊥DF. BD∩DF=D,∴DE⊥平面BDF.
又
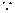 DE
DE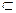 平面BDE,∴平面BDE⊥平面BDF.
平面BDE,∴平面BDE⊥平面BDF.(3)设点E和点A到平面PBC的距离分别为h1和h2.则
h1∶h2=EP∶AP=2∶3,
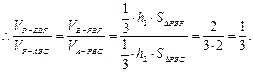
故截面BEF分三棱锥P—ABC所成两部分体积的比为1∶2或2∶1

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
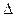 ABD和
ABD和 AC=
AC=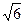 。
。
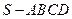 中,底面
中,底面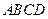 是正方形,
是正方形,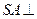 底面
底面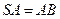 , 点
, 点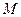 是
是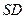 的中点,
的中点,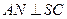 ,且交
,且交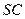 于点
于点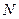 .
.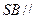 平面
平面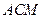 ;
;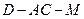 的余弦值大小;
的余弦值大小;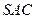 ⊥平面
⊥平面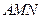 .
.
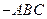 中
中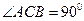 ,
,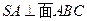 ,
,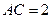 ,
,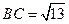 ,
,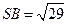 。
。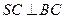 。
。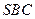 与底面
与底面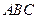 所成二面角的大小。
所成二面角的大小。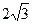 ,侧棱与底面所成的角为
,侧棱与底面所成的角为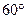 ,则该棱锥的体积为( )
,则该棱锥的体积为( )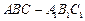 中,
中,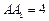 ,
,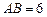 ,点
,点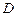 、
、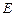 、
、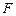 分别在棱
分别在棱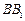 、
、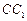 、
、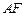 上,且
上,且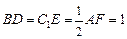 .
.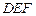 与平面
与平面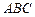 所成锐二面角的大小;
所成锐二面角的大小; 到平面
到平面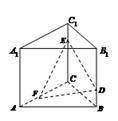
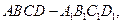
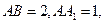
 直线
直线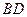 与平面
与平面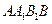 所成的角为
所成的角为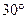 ,
,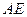 垂直
垂直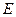 ,
,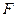 为
为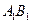 的中点.
的中点.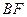 所成的角;
所成的角;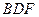 与平面
与平面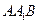 所成的二面角;
所成的二面角; 到平面
到平面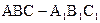 与正三棱锥
与正三棱锥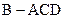 组成,其中,
组成,其中, .它的正视图、俯视图、从左向右的侧视图的面积分别为
.它的正视图、俯视图、从左向右的侧视图的面积分别为 ,
, .
.
 与平面
与平面 所成角的正弦;
所成角的正弦;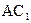 上是否存在点
上是否存在点 ,使
,使 平面
平面