题目内容
【题目】一名大学生尝试开家“网店”销售一种学习用品,经测算每售出1盒该产品可获利30元,未售出的商品每盒亏损10元.根据统计资料,得到该商品的月需求量的频率分布直方图如图所示,该同学为此购进180盒该产品,以x(单位:盒,100≤x≤200)表示一个月内的市场需求量,y(单位:元)表示一个月内经销该产品的利润.
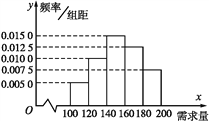
(1)根据直方图估计这个月内市场需求量x的平均数;
(2)将y表示为x的函数;
(3)根据直方图估计这个月利润不少于3 800元的概率(用频率近似概率).
【答案】（1）153；（2）
；（3）0.7
【解析】试题分析：（1）根据直方图能估计这个月内市场需求量
的平均数；（2）由每售出1盒盖产品获利30元，未售出的商品每盒亏损10元，分
，
两种情况进行分类讨论，能将
表示为的函数；（3）由利润不少于3800元，得到
，由此能求出利润不少于3800元的概率．
试题解析：(1)由频率分布直方图得:
需求量在[100,120)内的频率为0.005×20=0.1,
需求量在[120,140)内的频率为0.01×20=0.2,
需求量在[140,160)内的频率为0.015×20=0.3,
需求量在[160,180)内的频率为0.012 5×20=0.25,
需求量在[180,200]内的频率为0.007 5×20=0.15,
∴根据直方图估计这个月内市场需求量x的平均数为
=110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153.
(2)∵每售出1盒该产品获利30元,未售出的商品每盒亏损10元,
∴当100≤x<180时,y=30x-10(180-x)=40x-1 800;当180≤x≤200时,y=30×180=5 400.
∴y=
(3)∵利润不少于3 800元
∴40x-1 800≥3 800
∴x≥140
∴由(1)知利润不少于3 800元的概率为1-0.1-0.2=0.7.
