题目内容
已知椭圆: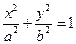 上一点
上一点 及其焦点
及其焦点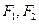 满足
满足

⑴求椭圆的标准方程。
⑵如图,过焦点F2作两条互相垂直的弦AB,CD,设弦AB,CD的中点分别为M,N。
①线段MN是否恒过一个定点?如果经过定点,试求出它的坐标,如果不经过定点,试说明理由;
②求分别以AB,CD为直径的两圆公共弦中点的轨迹方程。
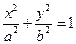 上一点
上一点 及其焦点
及其焦点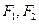 满足
满足

⑴求椭圆的标准方程。
⑵如图,过焦点F2作两条互相垂直的弦AB,CD,设弦AB,CD的中点分别为M,N。
①线段MN是否恒过一个定点?如果经过定点,试求出它的坐标,如果不经过定点,试说明理由;
②求分别以AB,CD为直径的两圆公共弦中点的轨迹方程。
 ,其轨迹是过定点
,其轨迹是过定点 的圆,MN恒过定点
的圆,MN恒过定点
解:⑴  ………………………3分
………………………3分
⑵①设直线AB的方程为: 并整理得:
并整理得:
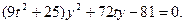
{007}设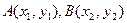 ,则有:
,则有:
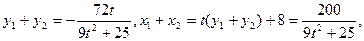
所以点 …………3分
…………3分
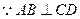 ,∴将t换成
,∴将t换成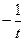 ,即得:
,即得: …………5分
…………5分
由两点式得直线MN的方程为

当y=0时, 所以直线MN恒过定点
所以直线MN恒过定点 。 …………7分
。 …………7分
②以弦AB为直径的圆M的方程为:
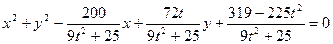 ①…………9分
①…………9分
又 将t换成
将t换成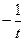 ,即得以弦CD为直径的圆N的方程为:
,即得以弦CD为直径的圆N的方程为:
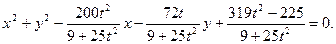 ②…………10分
②…………10分
①—②得两圆公共弦所在直线方程为: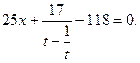 ③
③
又直线MN的方程为: ④…………12分
④…………12分
联解③④,消去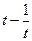 ,得两圆公共弦中点的轨迹方程为:
,得两圆公共弦中点的轨迹方程为:
 。
。
其轨迹是过定点 的圆。…………13分
的圆。…………13分
 ………………………3分
………………………3分⑵①设直线AB的方程为:
 并整理得:
并整理得: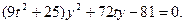
{007}设
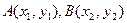 ,则有:
,则有: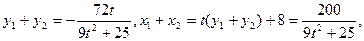
所以点
 …………3分
…………3分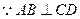 ,∴将t换成
,∴将t换成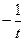 ,即得:
,即得: …………5分
…………5分由两点式得直线MN的方程为

当y=0时,
 所以直线MN恒过定点
所以直线MN恒过定点 。 …………7分
。 …………7分②以弦AB为直径的圆M的方程为:
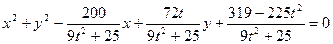 ①…………9分
①…………9分又
 将t换成
将t换成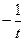 ,即得以弦CD为直径的圆N的方程为:
,即得以弦CD为直径的圆N的方程为: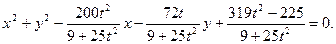 ②…………10分
②…………10分①—②得两圆公共弦所在直线方程为:
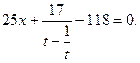 ③
③又直线MN的方程为:
 ④…………12分
④…………12分联解③④,消去
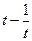 ,得两圆公共弦中点的轨迹方程为:
,得两圆公共弦中点的轨迹方程为: 。
。其轨迹是过定点
 的圆。…………13分
的圆。…………13分 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
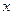 轴上,离心率为
轴上,离心率为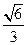 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为 ,过左准线与
,过左准线与 任作一条斜率不为零的直线
任作一条斜率不为零的直线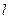 与椭圆W交于不同的两点
与椭圆W交于不同的两点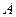 、
、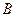 ,点
,点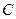 .
.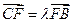 (
(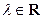 );
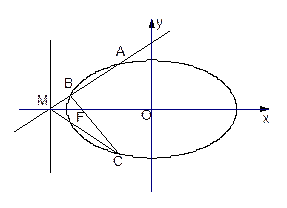
);
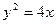 以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .
以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .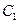 :
: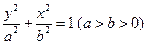 的右顶点为
的右顶点为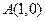 ,过
,过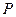 在抛物线
在抛物线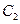 :
: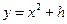
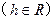 上,
上,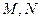 .线段
.线段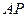 的中点与
的中点与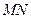 的中点的横坐标相等时,求
的中点的横坐标相等时,求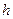 的最小值.
的最小值.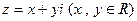 与复平面上点
与复平面上点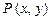 对应.
对应.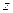 满足条件
满足条件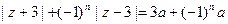 (其中
(其中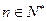 ,常数
,常数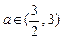 ),当
),当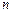 为奇数时,动点
为奇数时,动点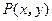 的轨迹为
的轨迹为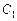 ;当
;当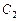 ,且两条曲线都经过点
,且两条曲线都经过点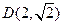 ,求轨迹
,求轨迹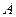 ,使点
,使点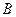
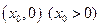 的最小距离不小于
的最小距离不小于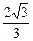 ,求实数
,求实数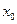 的取值范围.
的取值范围.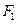 ,
,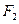 分别为椭圆
分别为椭圆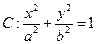
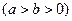 的左右焦点,过
的左右焦点,过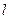 与椭圆
与椭圆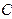 相交于
相交于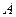 ,
,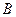 两点,直线
两点,直线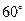 ,
,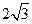 。
。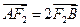 ,求椭圆
,求椭圆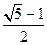 。类比“黄金椭圆”可推算出“黄金双曲线”的离心率e= 。
。类比“黄金椭圆”可推算出“黄金双曲线”的离心率e= 。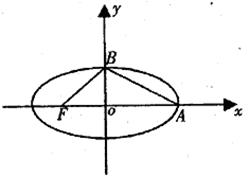
 分别是椭圆
分别是椭圆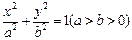 的上、下顶点和右焦点,直线
的上、下顶点和右焦点,直线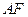 与椭圆的右准线交于点
与椭圆的右准线交于点 ,若直线
,若直线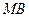 ∥
∥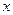 轴,则该椭圆的离心率
轴,则该椭圆的离心率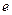 = ▲ .
= ▲ .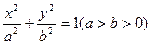 上存在一点M,它到左焦点的距离是它到右准线距离的2倍,则椭圆离心率的最小值为 .
上存在一点M,它到左焦点的距离是它到右准线距离的2倍,则椭圆离心率的最小值为 .