题目内容
已知命题p:方程(2x-a)(x+a)=0的两个根都在[-1,1]上;命题q:对任意实数x,不等式x2+2ax+2a≥0恒成立,若命题“p∧q”是真命题,求a的取值范围.
由(2x-a)(x+a)=0得x=
或x=-a,
∴当命题p为真命题时,-1≤
≤1且-1≤-a≤1,
解得-2≤a≤2且-1≤-a≤1,
∴-1≤a≤1,即p:-1≤-a≤1.
又当命题q为真命题时,“对任意实数x,不等式x2+2ax+2a≥0恒成立”
即抛物线y=x2+2ax+2a图象在x轴上方或者与x轴只有一个交点,
∴△=4a2-8a≤0,
∴0≤a≤2,即q:0≤a≤2.
若命题“p∧q”是真命题,则p为真命题且q为真命题,
∴0≤a≤1,即a的取值范围是[0,1].
| a |
| 2 |
∴当命题p为真命题时,-1≤
| a |
| 2 |
解得-2≤a≤2且-1≤-a≤1,
∴-1≤a≤1,即p:-1≤-a≤1.
又当命题q为真命题时,“对任意实数x,不等式x2+2ax+2a≥0恒成立”
即抛物线y=x2+2ax+2a图象在x轴上方或者与x轴只有一个交点,
∴△=4a2-8a≤0,
∴0≤a≤2,即q:0≤a≤2.
若命题“p∧q”是真命题,则p为真命题且q为真命题,
∴0≤a≤1,即a的取值范围是[0,1].

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
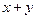 为有理数,则
为有理数,则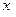 、
、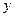 也都是有理数”;
也都是有理数”;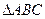 ∽
∽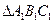 ”.
”.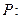 不等式
不等式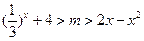 对一切实数
对一切实数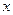 恒成立;命题
恒成立;命题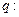 函数
函数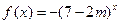 是
是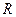 上的减函数. 若命题
上的减函数. 若命题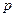 或
或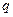 为真命题,命题
为真命题,命题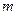 的取值范围是 .
的取值范围是 .