题目内容
设命题P：|m-5|≤3；命题Q：函数f（x）=3x2+2mx+m+
有两个不同的零点．求使命题“P或Q”为真命题的实数M的取值范围．
| 4 |
| 3 |
∵|m-5|≤3⇒2≤m≤8
命题P为真时，2≤m≤8
∵函数f（x）有两个不同的零点，∴△=4m2-12（m+
）＞0⇒m＞4或m＜-1
命题Q为真时，m＞4或m＜-1，
由复合命题真值表知：“P或Q”为真命题，则P、Q至少一个为真；
若P、Q都真，4＜m≤8，
若P、Q一真一假，（-∞，-1）∪[2，4]∪（8，+∞），
∴PⅤQ为真命题 m∈{m|m≥2或m＜-1}
命题P为真时，2≤m≤8
∵函数f（x）有两个不同的零点，∴△=4m2-12（m+
| 4 |
| 3 |
命题Q为真时，m＞4或m＜-1，
由复合命题真值表知：“P或Q”为真命题，则P、Q至少一个为真；
若P、Q都真，4＜m≤8，
若P、Q一真一假，（-∞，-1）∪[2，4]∪（8，+∞），
∴PⅤQ为真命题 m∈{m|m≥2或m＜-1}
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
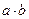不为零，则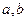
都不为零”的逆否命题是 。