题目内容
【题目】已知椭圆 
的右焦点到直线 
的距离为 
，离心率 
，A，B是椭圆上的两动点，动点P满足 
，（其中λ为常数）． 
（1）求椭圆标准方程；
（2）当λ=1且直线AB与OP斜率均存在时，求|kAB|+|kOP|的最小值；
（3）若G是线段AB的中点，且kOAkOB=kOGkAB ， 问是否存在常数λ和平面内两定点M，N，使得动点P满足PM+PN=18，若存在，求出λ的值和定点M，N；若不存在，请说明理由．
【答案】
（1）解：由题设可知：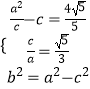 
，解得 
，b=2．
∴椭圆标准方程为 
（2）解：设A（x1，y1），B（x2，y2）则由 
，得P（x1+x2，y1+y2）．
∴ 
．
由|kAB|∈（0，+∞）得， 
，
当且仅当 
时取等号
（3）解：∵ 
= 
．
∴ 
．∴4x1x2+9y1y2=0．
设P（x，y），则由 ，
得（x，y）=（x1，y1）+λ（x2，y2）=（x1+λx2，y1+λy2），
即x=x1+λx2，y=y1+λy2．
∵点A、B在椭圆4x2+9y2=36上，
∴4x2+9y2=36+36λ2+2λ（4x1x2+9y1y2）．
∴4x2+9y2=36+36λ2．
即 
，
∴P点是椭圆 上的点，
设该椭圆的左、右焦点为M、N，
则由椭圆的定义PM+PN=18，得18= 
，
∴ 
， 
， 
．
∴存在常数λ= 
，和平面内两定点M（ 
，0），N（ 
，0），使得动点P满足PM+PN=18
【解析】（1）由已知列关于a，b，c的方程组，求解方程组可得椭圆标准方程；（2）设出A，B的坐标，把λ=1代入 ，求得P的坐标，求出AB、OP的斜率并作积，结合绝对值的不等式求解|kAB|+|kOP|的最小值；（3）设P（x，y），则由 ，得x=x1+λx2 ， y=y1+λy2 ． 再由点A、B在椭圆4x2+9y2=36上，得到 ，说明P点是椭圆 上的点，设该椭圆的左、右焦点为M、N，则由椭圆的定义PM+PN=18，得18= ，由此求得λ值．
