题目内容
【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，AB∥CD，∠ADC=90°，PD=AD=AB=1，DC=2．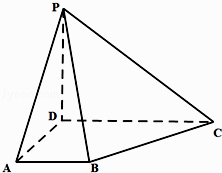 
（1）求证：BC⊥平面PBD；
（2）求二面角A﹣PB﹣C的大小．
【答案】
（1）证明：以D为原点建立空间直角坐标系D﹣xyz，如图所示，
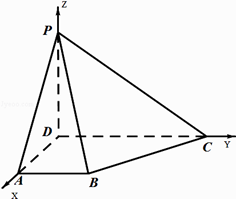
则：A（1，0，0），B（1，1，0），C（0，2，0），D（0，0，0），P（0，0，1）
∴ 
， 
， 
，
∴ 
，∴DP⊥BC，DB⊥BC，
又 DP平面PDB，DB平面PDB，DP∩DB=D，
∴BC⊥平面PBD
（2）由（1）可知： 
， 
， ．
设 
、 
分别是平面PAB和平面PBC的一个法向量，
则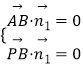 
且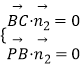 
即 
， 
不妨设x1=x2=1，则 
， 
，
∴ 
= 
．
由图已知二面角A﹣PB﹣C为钝二面角，
二面角A﹣PB﹣C的大小为 
．
【解析】（1）建立坐标系，求出 
， 
的坐标，通过计算数量积得出DP⊥BC，DB⊥BC，故BC⊥平面PBD；（2）分别求出两平面的法向量，计算法向量的夹角即可得出二面角的大小．
【考点精析】关于本题考查的直线与平面垂直的判定，需要了解一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案．
练习册系列答案
名校课堂系列答案
相关题目
