题目内容
【题目】已知函数f（x）=x2+2bx+c，且f（1）=f（3）=﹣1．设a＞0，将函数f（x）的图象先向右平移a个单位长度，再向下平移a2个单位长度，得到函数g（x）的图象． （Ⅰ）若函数g（x）有两个零点x1 ， x2 ， 且x1＜4＜x2 ， 求实数a的取值范围；
（Ⅱ）设连续函数在区间[m，n]上的值域为[λ，μ]，若有 
，则称该函数为“陡峭函数”．若函数g（x）在区间[a，2a]上为“陡峭函数”，求实数a的取值范围．
【答案】解：（Ⅰ）由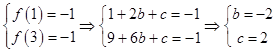 
，
即f（x）=x2﹣4x+2，…（1分）
由题设可知g（x）=（x﹣a）2﹣4（x﹣a）+2﹣a2=x2﹣（2a+4）x+4a+2，
因为g（x）有两个零点x1，x2，且x1＜4＜x2，
∴g（4）=16﹣4（2a+4）+4a+2＜0， 
，
又a＞0，于是实数a的取值范围为 
．
（Ⅱ）由g（x）=x2﹣（2a+4）x+4a+2可知，其对称轴为x=a+2，
①当0＜a≤2时，a+2≥2a，函数g（x）在区间[a，2a]上单调递减，
最小值λ=g（2a）=﹣4a+2，最大值μ=g（a）=﹣a2+2，
则 
，显然此时a不存在，
②当2＜a≤4时，a＜a+2＜2a，最小值λ=g（a+2）=﹣a2﹣2，
又 
，最大值μ=g（a）=﹣a2+2，则 
， 
，又2＜a≤4，此时a亦不存在，
③当a＞4时，a＜a+2＜2a，最小值λ=g（a+2）=﹣a2﹣2，
又 
，故最大值μ=g（2a）=﹣4a+2，
则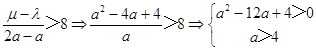 
， 
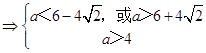，即 
，
综上可知，实数a的取值范围为 
．
【解析】（Ⅰ）由f（1）=f（3）=﹣1求出b，c值，得到函数f（x）的解析式，进而可得函数g（x）的解析式，由函数g（x）有两个零点x1，x2，且x1＜4＜x2，可得g（4）＜0，解得实数a的取值范围；（Ⅱ）根据已知中“陡峭函数”的定义，结合二次函数的图象和性质，分类讨论，可得满足条件的实数a的取值范围．
