题目内容
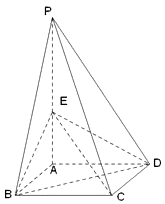
【题目】如图:四棱锥P﹣ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1, ![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 
(1)证明:当点E在边BC上移动时,总有EF⊥AF;
(2)当CE等于何值时,PA与平面PDE所成角的大小为45°.
【答案】
(1)证明:分别以AD、AB、AP所在直线为x、y、z轴,建立如图所示空间直角坐标系
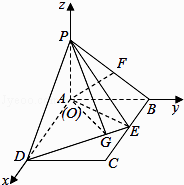
则可得P(0,0,1),B(0,1,0),F(0, ![]() ,
, ![]() ),D(
),D( ![]() ,0,0),
,0,0),
设BE=x,则E(x,1,0),∴ ![]() =(x,1,﹣1)
=(x,1,﹣1)
得 ![]() =x0+1×
=x0+1× ![]() +(﹣1)×
+(﹣1)× ![]() =0
=0
∴ ![]() ⊥
⊥ ![]() ,
,
∴当点E在边BC上移动时,总有EF⊥AF
(2)解: ![]() =(
=( ![]() ,0,﹣1),设平面PDE的一个法向量为
,0,﹣1),设平面PDE的一个法向量为 ![]() =(p,q,1),
=(p,q,1),
则 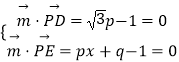 ,得
,得 ![]() =(
=( ![]() ,1﹣
,1﹣ ![]() ,1),
,1),
∵PA与平面PDE所成角的大小为45°, ![]() =(0,0,1),
=(0,0,1),
∴sin45°= 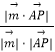 =
= ![]() ,得
,得 ![]() =
= ![]() ,
,
解得x= ![]() 或x
或x ![]() ,
,
∵BE=x ![]() ,
,
∴BE= ![]() ,即当CE等于
,即当CE等于 ![]() 时,PA与平面PDE所成角的大小为45°.
时,PA与平面PDE所成角的大小为45°.
【解析】(1)分别以AD、AB、AP所在直线为x、y、z轴,建立如图空间直角坐标系,利用向量法能证明当点E在边BC上移动时,总有EF⊥AF.(2)求出平面PDE的一个法向量,由此利用向量法能求出CE= ![]() 时,PA与平面PDE所成角的大小为45°.
时,PA与平面PDE所成角的大小为45°.
【考点精析】认真审题,首先需要了解空间中直线与直线之间的位置关系(相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点),还要掌握空间角的异面直线所成的角(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则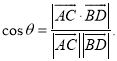 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

 应用题作业本系列答案
应用题作业本系列答案【题目】某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示. 
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | ① | 0.350 |
第3组 | [170,175) | 30 | ② |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185) | 10 | 0.100 |
合计 | 100 | 1.00 | |