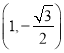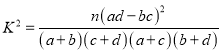题目内容
【题目】袋子中放有大小和形状相同而颜色互不相同的小球若干个, 其中标号为0的小球1个, 标号为1的小球1个, 标号为2的小球2个, 从袋子中不放回地随机抽取2个小球, 记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1) 记事件![]() 表示“
表示“![]() ”, 求事件
”, 求事件![]() 的概率;
的概率;
(2) 在区间![]() 内任取2个实数
内任取2个实数![]() , 记
, 记![]() 的最大值为
的最大值为![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
【答案】)(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)用列举法表示所有基本事件,数出满足“a+b=2”为事件A的个数,然后利用古典概型求解概率;
(2)直接利用几何概型,求解全部结果的区域面积与所求结果的区域面积,求解概率即可.
(1)不放回地随机抽取2个小球的所有基本事件个数有(0,1),(1,0),(0,21),(21,0),(0,22),(22,0),(1,21),(21,1),(1,22),(22,1),(21,22),(22,21)
记事件A表示“a+b=2”,有(0,21),(21,0),(0,22),(22,0),
∴事件A的概率P(A)![]() ,
,
(2)记“x2+y2<M”为事件B,
(a﹣b)2的最大值为M,则M=4,
则x2+y2<M”的概率等价于“x2+y2<4的概率”,
(x,y)可以看成平面中的点的坐标,
则全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域为B={(x,y)|x2+y2<4,(x,y)∈Ω}.
所以所求的概率为P(B)![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某电视台问政直播节目首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A部门 | 50% | 25% | 25% |
B部门 | 80% | 0 | 20% |
C部门 | 50% | 50% | 0 |
D部门 | 40% | 20% | 40% |

(1)若市民甲选择的是A部门,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的市民中再选出2人进行电视访谈,求这两人中至少有一人选择的是D部门的概率.
【题目】某单位鼓励员工参加健身运动,推广了一款手机软件,记录每人每天走路消耗的卡路里;软件的测评人员从员工中随机地选取了40人(男女各20人),记录他们某一天消耗的卡路里,并将数据整理如下:
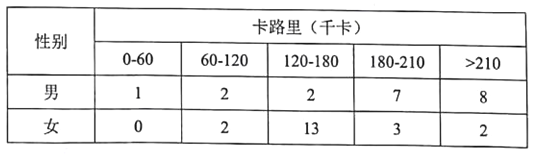
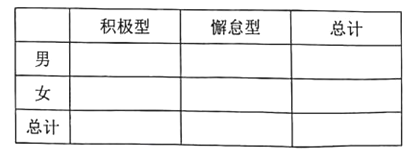
(1)已知某人一天的走路消耗卡路里超过180千卡被评测为“积极型”,否则为“懈怠型”,根据题中数据完成下面的![]() 列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
(2)若测评人员以这40位员工每日走路所消耗的卡路里的频率分布来估计其所有员工每日走路消耗卡路里的频率分布,现在测评人员从所有员工中任选2人,其中每日走路消耗卡路里不超过120千卡的有![]() 人,超过210千卡的有
人,超过210千卡的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 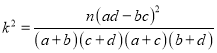 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人是饮食以蔬菜为主;饮食指数高于70的人是饮食以肉类为主.

(1)完成下列2×2列联表:

能否有99%的把握认为老师的饮食习惯与年龄有关?
(2)从群力校区任选一名老师, 设“选到45岁以上老师”为事件![]() , “饮食指数高于70的老师”为事件
, “饮食指数高于70的老师”为事件![]() , 用调查的结果估计
, 用调查的结果估计![]() 及
及![]() (用最简分数作答);
(用最简分数作答);
(3)为了给食堂提供老师的饮食信息, 根据(1)(2)的结论,能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()