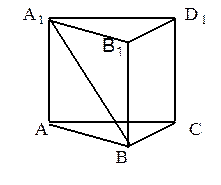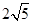题目内容
已知 ,
, ,
, 为三条不同的直线,
为三条不同的直线, ,
,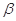 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( )
A. ⊥ ⊥ , , ⊥ ⊥ ,且 ,且 ,则 ,则 ⊥ ⊥ . . |
B.若平面 内有不共线的三点到平面 内有不共线的三点到平面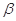 的距离相等,则 的距离相等,则 . . |
C.若 , , ,则 ,则 . . |
D.若 , , ,则 ,则 . . |
D
解析试题分析:由线面垂直的判定定理知A错;平面 与
与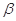 相交,三点在平面
相交,三点在平面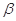 的两侧,故B错;C中,直线
的两侧,故B错;C中,直线 有可能在平面
有可能在平面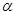 内,故选D。
内,故选D。
考点:(1)线面垂直的判断及性质定理;(2)面面平行的判定定理。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
M.N分别为正方体中棱BC和棱CC1的中点,则异面直线AC和MN所成的角为 ( )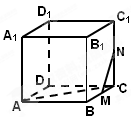
| A.30° | B.45° | C.60° | D.90° |
对于平面α和共面的直线m、n,下列命题正确的是( )
| A.若m、n与α所成的角相等,则m∥n |
| B.若m∥α,n∥α,则m∥n |
| C.若m⊥α,m⊥n,则n∥α |
D.若m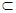 α,n∥α,则m∥n α,n∥α,则m∥n |
设m,n是两条不同的直线,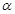 、
、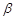 、
、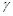 是三个不同的平面,给出下列命题,正确的是( ).
是三个不同的平面,给出下列命题,正确的是( ).
A.若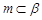 , ,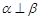 ,则 ,则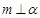 |
B.若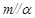 , ,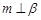 ,则 ,则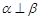 |
C.若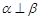 , ,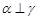 ,则 ,则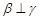 |
D.若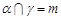 , ,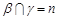 , , ,则 ,则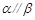 |
已知直线a,b异面, ,给出以下命题:①一定存在平行于a的平面
使 ;②一定存在平行于a的平面
;②一定存在平行于a的平面 使
使 ∥
∥ ;③一定存在平行于a的平面
;③一定存在平行于a的平面 使
使 ;④一定存在无数个平行于a的平面
;④一定存在无数个平行于a的平面 与b交于一定点.则其中论断正确的是( )
与b交于一定点.则其中论断正确的是( )
| A.①④ | B.②③ | C.①②③ | D.②③④ |
已知两条互不重合的直线m,n,两个不同的平面α,β,下列命题中正确的是( )
| A.若m∥α,n∥β,且m∥n,则α∥β |
| B.若m⊥α,n∥β,且m⊥n,则α⊥β |
| C.若m⊥α,n∥β,且m∥n,则α∥β |
| D.若m⊥α,n⊥β,且m⊥n,则α⊥β |
将图(1)中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图(2)),则在空间四面体ABCD中,AD与BC的位置关系是( )
| A.相交且垂直 | B.相交但不垂直 |
| C.异面且垂直 | D.异面但不垂直 |

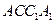 成45°角,AB=4cm,求这个棱柱的侧面积。(12分)
成45°角,AB=4cm,求这个棱柱的侧面积。(12分)