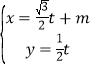题目内容
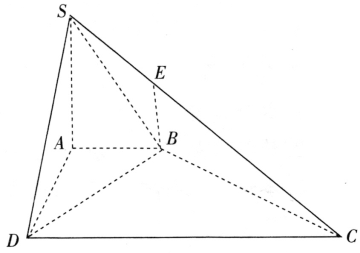
【题目】如图,在三棱锥P-ABC中,已知PC⊥BC,PC⊥AC,点E,F,G分别是所在棱的中点,则下面结论中错误的是 ( )

A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直线EF与直线PC所成的角
D.∠FEG是平面PAB与平面ABC所成二面角的平面角
【答案】D
【解析】
对于A,因为点E,F分别是AB,AP的中点,
所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .同理
.同理![]() 平面
平面![]() ,
,
又![]() ,
,
所以平面![]() 平面
平面![]() .因此A正确.
.因此A正确.
对于B,因为![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .因此B正确.
.因此B正确.
对于C,由于平面![]() 平面
平面![]() ,且与平面PAB交于EF,PB,∴
,且与平面PAB交于EF,PB,∴![]()
![]()
所以∠BPC是直线EF与直线PC所成的角.因此C正确.
对于D,由于FE,GE与AB不垂直,所以∠FEG不是平面PAB与平面ABC所成二面角的平面角,因此D不正确.
综上选项D不正确.选D.

练习册系列答案
相关题目
【题目】为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
(1)根据以上数据,能否有![]() 的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式与数据![]() 对应
对应![]() ,
,![]() 对应
对应![]() .
.