题目内容
【题目】已知函数y=f(x)是定义域为R的偶函数.当x≥0时, ,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据题意,由函数![]() 的解析式以及奇偶性分析可得
的解析式以及奇偶性分析可得![]() 的最小值与极大值,要使关于
的最小值与极大值,要使关于![]() 的方程
的方程![]() ,
,![]() 有且只有6个不同实数根,转化为
有且只有6个不同实数根,转化为![]() 必有两个根
必有两个根![]() 、
、![]() ,可得
,可得![]() ,根据韦达定理可得答案.
,根据韦达定理可得答案.
根据题意,当![]() 时,
时,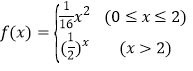 ,
,
![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,当
上递减,当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() ,
,
当![]() 时,函数
时,函数![]() 取得最小值0,
取得最小值0,
又由函数为偶函数,则![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() ,
,
当![]() 时,函数
时,函数![]() 取得最小值0,
取得最小值0,
要使关于![]() 的方程
的方程![]() ,有且只有6个不同实数根,
,有且只有6个不同实数根,
设![]() ,
,
则![]() 必有两个根
必有两个根![]() 、
、![]() ,
,
且必有![]() ,
,![]() 的图象与
的图象与![]() 的图象有两个交点,
的图象有两个交点,![]() 有两个根;
有两个根;
![]() ,
,![]() 的图象与
的图象与![]() 的图象有四个交点,
的图象有四个交点,![]() 由四个根,
由四个根,
关于![]() 的方程
的方程![]() ,有且只有6个不同实数根,
,有且只有6个不同实数根,
可得![]()
又由![]() ,
,
则有![]() ,即a的取值范围是
,即a的取值范围是![]() ,故选B.
,故选B.

练习册系列答案
相关题目


