题目内容
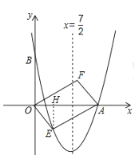
【题目】如图，对称轴为直线
的抛物线经过点
和
.
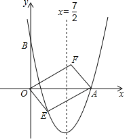
（1）求抛物线解析式及顶点坐标；
（2）设点
是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；
【答案】（1）解析式为
，此时顶点坐标为
（2）
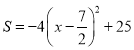，其中
【解析】
（1）根据题意，设抛物线的解析式为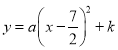
，将点
和
代入，列方程组，求解即可.
（2）过点E作
，垂足为H，由题意可知，
，即
，求解即可.
解：（1）由题可设抛物线的解析式为，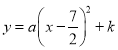
抛物线经过点和
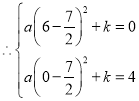，解得：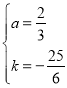
.
抛物线的解析式为，此时顶点坐标为.
（2）过点E作，垂足为H，如图.
由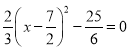
得
，
.
点
是抛物线上位于第四象限一动点，
，
.
四边形OEAF是平行四边形，
.
.
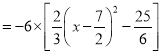
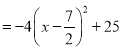四边形OEAF的面积S与x之间的函数关系式为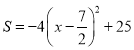，其中.
练习册系列答案
相关题目
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆)，若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
（1）求下表中z的值；
（2）用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下：94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数
记这8辆轿车的得分的平均数为
，定义事件
{
，且函数
没有零点}，求事件
发生的概率
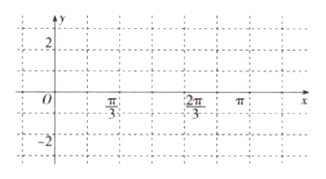
【题目】某同学用“五点法”画函数
在某一个周期内的图像时，列表并填入了部分数据，如下表：
|
|
| |||
| 0 |
|
|
|
|
| 0 | 3 | 0 | 0 |
（1）请将上表数据补充完整，并写出函数
的解析式（直接写出结果即可）；
（2）根据表格中的数据作出在一个周期内的图像；
（3）求函数在区间
上的最大值和最小值.
