Question

【题目】如图，在正四棱锥中，O为顶点S在底面ABCD内的投影，P为侧棱SD的中点，且.

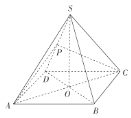
(1)证明:平面PAC.

(2)求直线BC与平面PAC的所成角的大小.

Answer 1

【答案】(1)见解析；(2)

【解析】

（1）连接OP，可得，利用线面平行的判定定理即可证出.

（2）以O为坐标原点，以OA所在直线为x轴，OB所在直线为y轴，OS所在直线为z轴，建立空间直角坐标系，设，求出平面PAC的一个法向量，利用向量的数量积结合图形即可求解.

(1)证明:连接OP，因为O，P分别为BD和SD的中点，所以，

又平面PAC，平面PAC，所以平面PAC.

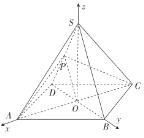
(2)解:如图，以O为坐标原点，以OA所在直线为x轴，OB所在直线为y轴，

OS所在直线为z轴，建立空间直角坐标系.

设，

则，，，，

则，，.

设平面PAC的一个法向量为，

则，，

所以，令，得，

所以

所以

故直线BC与平面PAC的夹角为.