题目内容
【题目】已知函数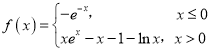 ,则函数
,则函数![]() 的零点个数为( )(
的零点个数为( )(![]() 是自然对数的底数)
是自然对数的底数)
A.6B.5C.4D.3
【答案】B
【解析】
利用导数研究函数![]() 的性质,如单调性,函数值的变化趋势和,函数的极值.再研究方程
的性质,如单调性,函数值的变化趋势和,函数的极值.再研究方程![]() 的解的个数,即直线
的解的个数,即直线![]() 与函数
与函数![]() 的公共点的的取值,从而利用函数
的公共点的的取值,从而利用函数![]() 的性质求得
的性质求得![]() 零点个数.
零点个数.
![]() 时,
时,![]() 是增函数,
是增函数,![]() ,
,
![]() 时,
时,![]() ,
,![]() ,显然
,显然![]() ,
,
由![]() ,
,
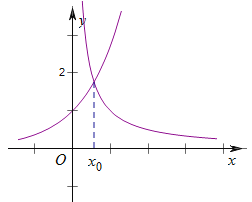
作出![]() 和
和![]() 的图象,如图,
的图象,如图,![]() 是增函数,
是增函数,![]() 在
在![]() 是减函数
是减函数
它们有一个交点,设交点横坐标为![]() ,易得
,易得![]() ,
,![]() ,
,
在![]() 时,
时,![]() ,
,![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,![]() 是
是![]() 的极小值,也是在
的极小值,也是在![]() 时的最小值.
时的最小值.![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() 时,
时,![]() .作出
.作出![]() 的大致图象,作直线
的大致图象,作直线![]() ,如图,
,如图,![]() 时
时![]() 与
与![]() 的图象有两个交点,即
的图象有两个交点,即![]() 有两个解
有两个解![]() ,
,![]() .
.
![]() 时,
时,![]() ,
,![]() ,由
,由![]() 得
得![]() ,而
,而![]() 时,
时,![]() ,
,![]() ,所以直线
,所以直线![]() 与
与![]() 在
在![]() 处相切.即
处相切.即![]() 时方程
时方程![]() 有一个解
有一个解![]() .
.
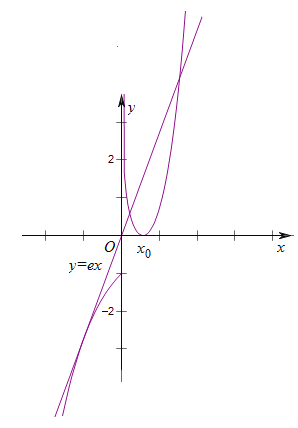
![]() ,令
,令![]() ,则
,则![]() ,由上讨论知方程
,由上讨论知方程![]() 有三个解:
有三个解:![]() (
(![]() )
)
而![]() 有一个解,
有一个解,![]() 和
和![]() 都有两个解,所以
都有两个解,所以![]() 有5个解,
有5个解,
即函数![]() 有5个零点.
有5个零点.
故选:B.

练习册系列答案
相关题目