题目内容
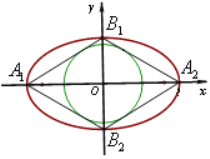
【题目】设椭圆![]()
![]() (
(![]() )的左右顶点为
)的左右顶点为![]() ,上下顶点为
,上下顶点为![]() ,菱形
,菱形![]() 的内切圆
的内切圆![]() 的半径为
的半径为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆上关于原点对称的两点,椭圆上一点
是椭圆上关于原点对称的两点,椭圆上一点![]() 满足
满足![]() ,试判断直线
,试判断直线![]() 与圆
与圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
【答案】(1)![]() (2)直线
(2)直线![]() 、
、![]() 与圆
与圆![]() 相切,证明见解析
相切,证明见解析
【解析】
(1)由离心率得![]() ,用两种方法表示出菱形
,用两种方法表示出菱形![]() 的面积可求得
的面积可求得![]() ,得椭圆方程;
,得椭圆方程;
(2)设![]() ,
,![]() .当直线
.当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,用韦达定理得
,代入椭圆方程,用韦达定理得![]() ,利用
,利用![]() ,即
,即![]() 得
得![]() 的关系,求出圆心
的关系,求出圆心![]() 到直线
到直线![]() 的距离可得直线与圆的位置关系.直线
的距离可得直线与圆的位置关系.直线![]() 的斜率不存在时,直接计算可得,由对称性
的斜率不存在时,直接计算可得,由对称性![]() 的结论也可得.
的结论也可得.
(1)设椭圆的半焦距为![]() .由椭圆的离心率为
.由椭圆的离心率为![]() 知,
知,![]() .
.
设圆![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
∴![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的方程为
的方程为![]()
(2)∵![]() 关于原点对称,
关于原点对称,![]() ,∴
,∴![]() .
.
设![]() ,
,![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由直线和椭圆方程联立得![]() ,即
,即![]() ,
,
∴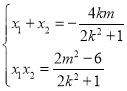 .
.
∵![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴圆![]() 的圆心O到直线
的圆心O到直线![]() 的距离为
的距离为![]() ,∴直线
,∴直线![]() 与圆
与圆![]() 相切.
相切.
当直线![]() 的斜率不存在时,依题意得
的斜率不存在时,依题意得![]() ,
,![]() .
.
由![]() 得
得![]() ,∴
,∴![]() ,结合
,结合![]() 得
得![]() ,
,
∴直线![]() 到原点O的距离都是
到原点O的距离都是![]() ,
,
∴直线![]() 与圆
与圆![]() 也相切.
也相切.
同理可得,直线![]() 与圆
与圆![]() 也相切.
也相切.
∴直线![]() 、
、![]() 与圆
与圆![]() 相切
相切

练习册系列答案
相关题目
【题目】某农场为了提高某品种水稻的产量,进行良种优选,在同一试验田中分两块种植了甲乙两种水稻.为了比较甲乙两种水稻的产量,现从甲乙两种水稻中各随机选取20株成熟水稻.根据每株水稻颗粒的重量(单位:克)绘制了如下茎叶图:
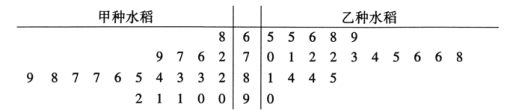
(1)根据茎叶图判断哪种水稻的产量更高?并说明理由;
(2)求40株水稻颗粒重量的中位数![]() ,并将重量超过
,并将重量超过![]() 和不超过
和不超过![]() 的水稻株数填入下面的列联表:
的水稻株数填入下面的列联表:
超过 | 不超过 | |
甲种水稻 | ||
乙种水稻 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种水稻的产量有差异?附:
的把握认为两种水稻的产量有差异?附: ;
;
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |