题目内容
【题目】若动点![]() 到两点
到两点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 上一点,过点
上一点,过点![]() 作曲线
作曲线![]() 的切线与椭圆
的切线与椭圆![]() 交于另一点
交于另一点![]() ,求
,求![]() 面积的取值范围(
面积的取值范围(![]() 为坐标原点).
为坐标原点).
【答案】(1)![]() ;(2)
;(2)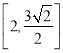 .
.
【解析】
(1)设![]() ,由两点间距离公式并结合条件化简即可求得动点
,由两点间距离公式并结合条件化简即可求得动点![]() 的轨迹方程.
的轨迹方程.
(2)讨论直线![]() 的斜率是否存.当斜率不存在时,易得
的斜率是否存.当斜率不存在时,易得![]() ;当斜率存在时,设
;当斜率存在时,设![]() 的方程为
的方程为![]() ,结合点到直线距离公式及切线性质可知
,结合点到直线距离公式及切线性质可知![]() 到
到![]() 的距离
的距离![]() .联立椭圆方程,由韦达定理可得
.联立椭圆方程,由韦达定理可得![]()
![]() .结合弦长公式表示出
.结合弦长公式表示出![]() .利用换元法求得
.利用换元法求得![]() 的取值范围,即可求得
的取值范围,即可求得![]() 面积的取值范围.
面积的取值范围.
(1)设![]() ,由条件可知
,由条件可知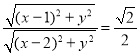 ,
,
即![]() ,
,
所以曲线![]() .
.
(2)当![]() 所在直线斜率不存在时,其方程为
所在直线斜率不存在时,其方程为![]() ,此时
,此时![]() ,
,
当![]() 所在直线斜率存在时,设其方程为
所在直线斜率存在时,设其方程为![]() ,设
,设![]() ,
,![]() ,
,
![]() 到直线
到直线![]() 的距离
的距离![]() ,即
,即![]() ,所以
,所以![]() .
.
直线![]() 与椭圆
与椭圆![]() 联立
联立 ,
,
得![]() ,
,
所以![]()
![]()
所以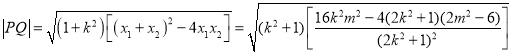

令![]() ,
,![]()
![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以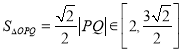 .
.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【题目】已知椭圆![]() ,
,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, 为椭圆上一点,
为椭圆上一点,![]() 的离心率
的离心率![]()
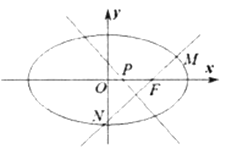
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 过点
过点![]() 交椭圆
交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,试探究
,试探究![]() 是否为定值,如果是,请求出该定值;如果不是,请说明理由.
是否为定值,如果是,请求出该定值;如果不是,请说明理由.
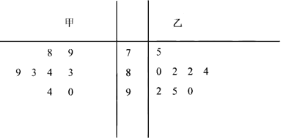
【题目】某农场为了提高某品种水稻的产量,进行良种优选,在同一试验田中分两块种植了甲乙两种水稻.为了比较甲乙两种水稻的产量,现从甲乙两种水稻中各随机选取20株成熟水稻.根据每株水稻颗粒的重量(单位:克)绘制了如下茎叶图:
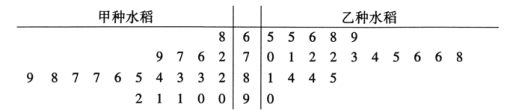
(1)根据茎叶图判断哪种水稻的产量更高?并说明理由;
(2)求40株水稻颗粒重量的中位数![]() ,并将重量超过
,并将重量超过![]() 和不超过
和不超过![]() 的水稻株数填入下面的列联表:
的水稻株数填入下面的列联表:
超过 | 不超过 | |
甲种水稻 | ||
乙种水稻 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种水稻的产量有差异?附:
的把握认为两种水稻的产量有差异?附: ;
;
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |