Question

【题目】已知四面体有五条棱长为3，且外接球半径为2.动点P在四面体的内部或表面，P到四个面的距离之和记为s.已知动点P在，两处时，s分别取得最小值和最大值，则线段长度的最小值为______.

Answer 1

【答案】

【解析】

设四面体为,其中，取的中点分别为，求出的长，将点到四个面的距离之和记为s，转化为到其中两个面的距离，利用等体积的方法分析出距离之和的最值，从而得到线段长度的最小值为，上两点间的距离的最小值，得到答案.

四面体为,其中,设.

取的中点分别为，连接 ,如图.

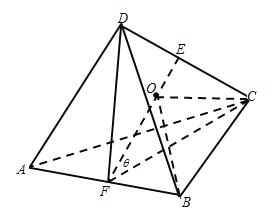
在等腰三角形中，有.

所以平面，又为的中点.

则四面体的外接球的球心一定在平面 上.

同理可得四面体的外接球的球心一定在平面上.

所以四面体的外接球的球心一定在上.

连接，设.

在直角三角形中，.

在三角形中，.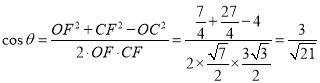

在直角三角形中,.

所以长为定值，的长为定值.

根据条件有,设为, ,设为

设点到四个面,,,的距离分别为.

设四面体的体积为(为定值)

由等体积法有：

所以

所以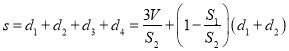

当点在上时，最小.

当点远离时，的值增大，

由等体积法可得当点在上时，的值相等，且此时的值最大.

所以当点在或上时，取得最值.

故线段长度的最小值为，上两点间的距离的最小值.

由上可知，.

所以，上两点间的距离的最小值为.

故答案为：.