Question

【题目】设区间，定义在上的函数（），集合．

（1）若，求集合；

（2）设常数．

① 讨论的单调性；

② 若，求证：．

Answer 1

【答案】（1）（2）①见解析；②见证明

【解析】

（1）把b代入函数解析式，求出导函数，由f′（x）0，可知f（x）在[﹣3，3]上为增函数，求出函数的最小值，由最小值大于0求得a的取值范围；

（2）①求出函数的导函数，解得导函数的零点，然后根据与3的关系分类求得函数的单调区间；

②当b＜﹣1时，由①可知，当0＜a时，求得函数的最小值小于0，得到矛盾，故此时实数a不存在；当a时，由①可得f（x）min＝{f（﹣3），f（）}，得到f（﹣3）＜0，这与x∈D，f（x）≥0恒成立矛盾，故此时实数a不存在；若f（﹣3）＞0，证明f（）＜0，这与x∈D，f（x）≥0恒成立矛盾，故此时实数a不存在．

（1）当时，，则．

由可知恒成立，故函数在上单调递增，

所以，解得，

所以集合

（2）① 由得，

因为，则由，得．

在上列表如下：

	＋	0	－	0	＋
	单调递增	极大值	单调递减	极小值	单调递增

（ⅰ）当，即时，

则，所以在上单调递减；

（ⅱ）当，即时，此时，

在和上单调递增；在上单调递减．

综上，当时，在上单调递减；

当时，在，上单调递增；

在上单调递减

②（方法一）当时，由①可知，

（ⅰ）当时，在上单调递减，

所以，

这与恒成立矛盾，故此时实数不存在；

（ⅱ）当时，在，上单调递增；

在上单调递减，

所以．

若，这与恒成立矛盾，

故此时实数不存在；

若，此时，

又，则，

．

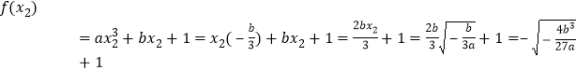下面证明，也即证：．

因为，且，则，

下证：．

令，则，

所以在上单调递增，所以，即．

这与恒成立矛盾，故此时实数不存在．

综上所述，．

（方法二）（ⅰ）当时，成立；

（ⅱ）当时，由题意可知恒成立，则，

设，则，

令，解得．

因为，所以，

所以在上单调递增，在上单调递减，

所以，所以；

（ⅲ）当时，由题意可知恒成立，则．

设，则，

因为，所以恒成立，所以在上单调递增，

所以，

所以．

若，则存在实数满足，

则成立，即，

也即成立，

则，这与矛盾，所以．