Question

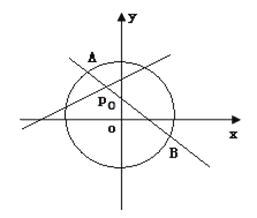
【题目】已知圆O：x2+y2＝8内有一点P0（﹣1，2），AB为过点P0且倾斜角为α的弦．

（1）当α＝135°时，求弦AB的长；

（2）当弦AB被P0平分时，求直线AB的方程．

Answer 1

【答案】（1）（2）x﹣2y+5＝0

【解析】

（1）依题意直线AB的斜率为﹣1，直线AB的方程，根据圆心0（0，0）到直线AB的距离，由弦长公式求得AB的长．

（2）当弦AB被点P0平分时，AB和OP垂直，故直线AB 的斜率为，根据点斜式方程直线AB的方程．

解：（1）当α＝135°时，kAB＝﹣1，直线AB：y+2＝﹣（x﹣1），即x+y+1＝0

设AB中点为M，则OM⊥AB，且平分弦AB．

∵，

∴，

∴．

（2）当弦AB被点P平分时，OP⊥AB，而kOP＝﹣2，

∴．

∴弦AB所在直线的方程为：x﹣2y+5＝0．