题目内容
已知函数 ,其中
,其中 .
.
(1)当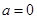 时,求函数
时,求函数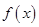 的图象在点
的图象在点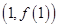 处的切线方程;
处的切线方程;
(2)如果对于任意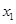 、
、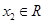 ,且
,且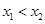 ,都有
,都有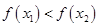 ,求
,求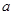 的取值范围.
的取值范围.
 ,其中
,其中 .
.(1)当
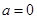 时,求函数
时,求函数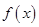 的图象在点
的图象在点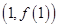 处的切线方程;
处的切线方程;(2)如果对于任意
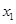 、
、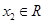 ,且
,且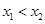 ,都有
,都有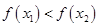 ,求
,求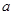 的取值范围.
的取值范围.(1)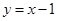 ;(2)
;(2) .
.
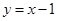 ;(2)
;(2) .
.试题分析:(1)将
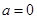 代入函数
代入函数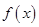 的解析式,求出切点坐标与
的解析式,求出切点坐标与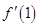 ,再利用点斜式写出相应的切线方程;(2)将问题等价于
,再利用点斜式写出相应的切线方程;(2)将问题等价于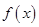 在
在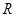 上单调递增来处理,然后分别考虑函数
上单调递增来处理,然后分别考虑函数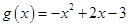 和
和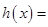
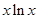 的单调性与极值,利用两个函数的图象确定直线
的单调性与极值,利用两个函数的图象确定直线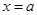 的位置,利用
的位置,利用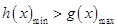 来进行限制,从而求解出实数
来进行限制,从而求解出实数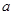 的取值范围.
的取值范围.试题解析:(1)由题意,得
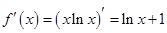 ,其中
,其中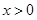 ,
,所以
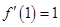 ,
,又因为
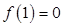 ,
,所以函数
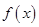 的图象在点
的图象在点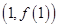 处的切线方程为
处的切线方程为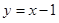 ;
;(2)先考察函数
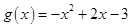 ,
,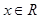 的图象,
的图象,配方得
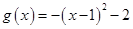 ,
,所以函数
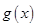 在
在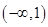 上单调递增,在
上单调递增,在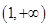 单调递减,且
单调递减,且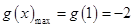 .
.因为对于任意
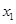 、
、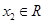 ,且
,且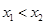 ,都有
,都有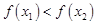 成立,
成立,所以
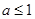 .
.以下考察函数
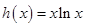 ,
,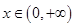 的图象,
的图象,则
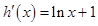 ,
,令
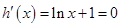 ,解得
,解得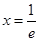 .
.随着
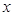 变化时,
变化时,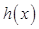 和
和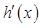 的变化情况如下:
的变化情况如下: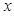 | 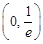 | 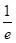 | 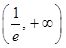 |
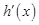 | 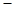 | 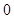 | 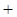 |
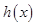 | ↘ | | ↗ |
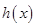 在
在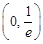 上单调递减,在
上单调递减,在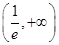 上单调递增,且
上单调递增,且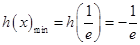 .
.因为对于任意
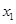 、
、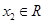 ,且
,且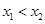 ,都有
,都有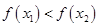 成立,
成立,所以
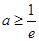 .
.因为
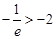 (即
(即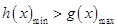 ),
),所以
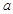 的取值范围为
的取值范围为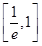 .
.
练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 ,对任意
,对任意 ,都有
,都有
 .
.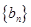 满足
满足 ,求数列
,求数列 .
.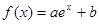 在
在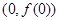 处切线为
处切线为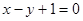 .
.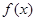 的解析式;
的解析式;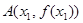 ,
,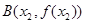 ,
,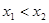 ,
,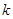 表示直线
表示直线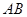 的斜率,求证:
的斜率,求证: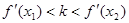 .
. :
:
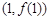 处的切线方程;
处的切线方程; 平行的曲线C的切线方程.
平行的曲线C的切线方程. 的导数
的导数 ,则数列
,则数列 的前n项和( )
的前n项和( )



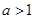 ,且函数
,且函数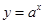 与函数
与函数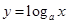 的图象有且仅有一个公共点,则此公共点的坐标为 .
的图象有且仅有一个公共点,则此公共点的坐标为 .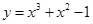 在点
在点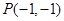 处的切线方程是
处的切线方程是  在
在 处的切线方程是( )
处的切线方程是( )






